The Keyboard

We have met all the symbols shown in the score detail above, except for the key signature, but music means nothing to most of us until it has been translated into the sounds produced by a musical instrument.

Teachers of music theory recommend that you should master the rudiments of a musical instrument if you want to understand why music is notated the way it is. In particular, if you wish to study harmony, you should consider learning an instrument capable of playing harmony, for example, a plucked string instrument (guitar, lute, harp) or a keyboard instrument (piano, organ). The structure of scales and chords becomes much clearer if you know your way around some kind of music keyboard.

A keyboard is made of keys that have been arranged in the pattern we have illustrated above. To make the pattern clearer, and to show the way the pattern repeats, we have coloured all the notes 'C' yellow, and, in addition, marked 'middle C' with an asterix. The pitch of any note is lower than that of all the keys to its right and higher than all those to its left. The white keys bear the names of the letters of the alphabet (A, B, C, D, E, F, G) and are called 'naturals'. Thus, the key bearing the letter 'A' plays the note 'A natural' on our keyboard. In normal speech, the description 'natural' may often be omitted and the note just called 'A'.

We show below this pattern transcribed onto a stave. Note that the note 'middle C' has been written twice, once on each line.

So far we have named only the white keys, the notes we call 'natural'. The black notes take their names from the white keys on either side on them. We have enlarged a portion of the keyboard, starting from 'middle C', to make this clearer. A black key immediate to the right of a white key is said to be sharp while a black key immediate to the left of a white key is said to be flat. Because every black key has a white key on either side of it, it bears two names. These are both shown on the diagram below. C sharp and D flat are the same key and will produce the same note when played on a keyboard.

Below we show this pattern transcribed onto a stave. It is an example of a scale (from the Latin scala meaning a ladder); in this case, a chromatic scale. We have written the scale twice. On the upper stave we have used the natural sign for the white keys and the sharp sign for the black keys. On the lower stave we have used the natural sign for the white keys and the flat sign for the black keys.

It is a convention to use sharps when writing out a rising chromatic scale and flats when writing out a falling chromatic scale. There are other ways of writing both rising and falling chromatic scales which we will consider in a later lesson.

The keyboard convention that naturals are faced in white and accidentals are faced in black was commonly reversed during the seventeenth and eighteenth centuries. Harpsichord keyboards, for example, commonly have white (bone or ivory) sharps with black (ebony) or yellow (boxwood) naturals. It was only with the introduction of the piano in the eighteenth century that the current convention became widely established.

We have no evidence that the convention for colouring musical keyboards was arrived at with any of the angst created when choosing the colours for computer keyboards that the story below, first printed in the San Jose Mercury News, describes.

Thoughts on Piano Keyboard Design

This is taken from Piano Keys on www.mathpages.com.

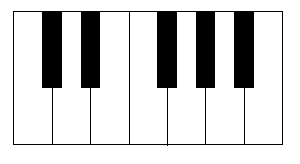
If you've ever looked closely at a piano keyboard you may have noticed that the widths of the white keys are not all the same at the back ends (where they pass between the black keys). Of course, if you think about it for a minute, it's clear they couldn't possibly all be the same width, assuming the black keys are all identical (with non-zero width) and the white keys all have equal widths at the front ends, because the only simultaneoussolution of 3W=3w+2b and 4W=4w+3b is with b=0.

After realizing this I started noticing different pianos and how they accommodate this little problem in linear programming. Let W denote the widths of the white keys at the front, and let B denote the widths of the black keys. Then let a, b,..., g (assigned to their musical equivalents) denote the widths of the white keys at the back. Assuming a perfect fit, it's impossible to have a = b = ... = g. The best you can do is try to minimize the greatest difference between any two of these keys.

One crude approach would be to set d=g=a=(W-B) and b=c=e=f=(W-B/2), which gives a maximum difference of B/2 between the widths of any two white keys (at the back ends). This isn't a very good solution, and I've never seen an actual keyboard based on this pattern (although some cartoon pianos seems to have this pattern). A better solution is to set a=b=c=e=f=g=(W-3B/4) and d=(W-B/2). With this arrangement, all but one of the white keys have the same width at the back end, and the discrepancy of the "odd" key (the key of "d") is only B/4. Some actual keyboards (e.g., the Roland HP-70) use this pattern.

Another solution is to set c=d=e=f=b=(W-2B/3) and g=a=(W-5B/6), which results in a maximum discrepancy of just B/6. There are several other combinations that give this same maximum discrepancy, and actual keyboards based on this pattern are not uncommon.

If we set c=e=(W-5B/8) and a=b=d=f=g=(W-3B/4) we have a maximum discrepancy of only B/8, and quite a few actual pianos use this pattern as well. However, the absolute optimum arrangement is to set c=d=e=(W-2B/3) and f=g=a=b=(W-3B/4), which gives a maximum discrepancy of just B/12. This pattern is used on many keyboards, e.g. the Roland PC-100.

The "B/12 solution" is best possible, given that all the black keys are identical and all the white keys have equal widths at the front ends. For practical manufacturing purposes this is probably the best approach. However, suppose we relax those conditions and allow variations in the widths of the black keys and in the widths of the white keys at the front ends. All we require is that the black keys (in total) are allocated 5/12 of the octave. On this basis, what is the optimum arrangement, minimizing the maximum discrepancy between any two widths of the same type?

Let A, B,...G denote the front-end widths of the white keys, and let a#, c#, d#, f#, g# denote the widths of the black keys. I believe the optimum arrangement is given by dividing the octave into 878472 units, and then setting

f=g=a=b=72156 units
c=d=e=74606 units
discrepancy=2450

f#=g#=a#=72520 units
c#=d#=74235 units
discrepancy=1715

F=G=A=B=126546 units
C=D=E=124096 units
discrepancy=2450

The maximum discrepancy between any two widths of the same class is 1/29.88 of the width of the average black key, which is less than half the discrepancy for the "B/12 solution".

The max discrepancy is 1/358.56 of the total octave for the white keys, and 1/512.22 for the black keys. Since an octave is normally about 6.5 inches, the max discrepancy is about 0.0181 inches for the white keys and 0.0127 inches for the black keys. (One peculiar fact about this optimum arrangement is that the median point of the octave, the boundary between f and f#, is exactly 444444 units up from the start of the octave.)

References:

• Keys and Keyboards, Odd Keyboards, The Keyboard Compass
• Piano Nanny - free piano lessons online