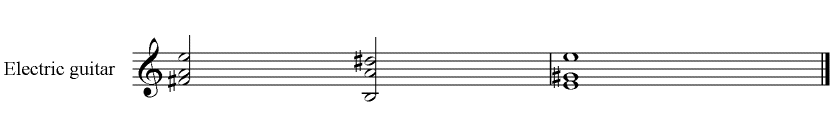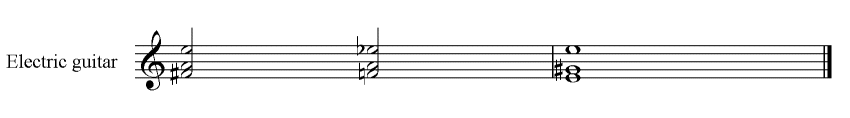|
The Nature of Tonality
::

|
Key word:
tonality |
| 1 |
The Nature of Tonality
Carol Krumhansl and Ed Kessler, using the 'probe tone technique' (developed by Roger Shepard) to study the nature of tonality, played a passage consisting of an ascending (major or harmonic minor) scale, or a chord progression. After each repetition of the key-defining passage, a different note was played. Listeners were asked to judge how well the note fitted the 'tonality' of the previous passage. Krumhansl and Kessler found a stable, distinctive response pattern for the major and minor keys. In both cases, the tonic note was rated most highly, and non-scale notes were rated the lowest. More specifically, a four-level hierarchy was evident for both the major and minor keys.
| 1 | the most important pitch is the tonic |
| 2 | followed by the remaining notes of the tonic triad (i.e. dominant and mediant) |
| 3 | followed by the other notes belonging to the scale |
| 4 | followed by the non-scale notes |
The Krumhansl and Schmuckler algorithm, based on Krumhansl and Kessler's work, is a technique for estimating the key of some arbitrary musical passage. The technique makes use of the profiles set out in the table above. The algorithm works as follows. Without regard for enharmonic spellings or octaves, all notes in the passage are counted, resulting in 12 values, one for each of the twelve notes in the equal-temperament chromatic scale. For example, let us consider a passage that contains 14 Cs, 2 C#s, 8 Ds, and so on. These 12 values are then correlated with the major key profile where C is deemed the tonic. Similarly, the 12 values are then correlated with the minor key profile where C is deemed the tonic. The process is repeated for all possible tonics: C sharp/D flat, D, D sharp/E flat, E, etc. After correlations have been calculated for all 24 keys, 12 major and 12 minor, the key for the passage is estimated to be that with the largest positive correlation.
The results found using the Krumhansl and Kessler algorithm appear to reflect tonality judgements made by listeners hearing the same passage. The algorithm appears to be about 85% correct for common musical passages. Maybe we sense the 'key' of a piece of tonal music in a similar way?
Somewhat different, but still endlessly fascinating, are the many theoretical works of the eighteenth century that explicitly assign certain affectations or emotional characteristics to different keys even if they often fail to agree just what these are. Paralleling this, other musicians associate different colours with different keys, an example of synesthesia. Both these topics are considered further in the reference below.
Reference:
|
| 2 |
What Makes Music Tonal?
The strictest definition of 'tonal music' is that it is based on principles of tonal relationship/tonal harmony, which arguably might be reduced to the use made of the tonic-dominant-subdominant relationship, which provides the need, and the mechanism, for resolution to the tonic.
This 'rule' is weakened by the observation that quartal music may have a tonicized 'tonal centre' but it is not 'tonal music'.
Likewise, modal music, has a 'tonal centre' but is not strictly speaking 'tonal music' because its harmonic rules are based on the relationships of certain key tones of each different mode rather than strictly on the tonic-dominant-subdominant relationship (indeed, some modes have no subdominant-dominant relationship at all).
Wagner's music is largely 'atonal' because he freed harmony from the stricture of the dominant-subdominant relationship. His music always returned to 'tonal' relationships when he was reinforcing the arrival of his target tonic, but otherwise, he avoided the all important dominant-subdominant relationship so as to blur and disguise any possible passing tonics.
The term 'atonal' is too often confused with 'dissonant', which is a relative term except when it comes to counterpoint, where is refers only to intervals between two voices, and covers seconds, sevenths, and tritones (and their octave extensions). The interval of a perfect fourth was also considered a dissonance when it occured between the bass and another voice.
So, to summarize, music can not 'seem' atonal/tonal... it either is or is not.
Music, aside from the rules of strict counterpoint, can 'seem' dissonant. However, this is a perfectly relative and subjective question of perception.
Reference:
- NorthernSounds.com - the above material quotes from forum submissions by Michel R. Edward and Jamie Kowalski
|
|
|
Major Keys
::

|
Key words:
major keys
key centre |
| 1 |
Major Keys
Popular music has a strong sense of key - pre-renaissance, late nineteenth- and early twentieth-century classical music often does not, being polytonal (many keys) or atonal (no key).
The analysis of a piece of music to determine its key is related to the way it 'sounds' and to this alone. If the notation leads you to 'see' the music in one key, but the sound tells quite another story, the notation is deficient. This is why we have stressed the need to follow a 'convention', a 'set of rules', directed towards reproducing on the page what you will 'hear' when the music is performed. There are occasions when these 'conventions' may be pushed to their limit but, in most cases, the 'convention' represents 'best practice'.
In the previous lesson we examined music notation for the guitar. If we are using only chord charts and chord numbering, we will be unaware of the key. There is no key signature. If we can 'hear' the chords in our head before we 'play' them. something well-trained and experienced musicians do as a matter of course, then this might point to the key. However, in the absence of this kind of 'cue' we can use the fact that particular groups of chords will be more likely in one key than another. The chords themselves can be an excellent pointer to finding the key centre, the key at that point in the piece. Of course, it is the tonic chord, not the tonic note, that establishes the key centre. The best method for finding the key centre of a progression of chords is to list possible keys to which each chord can belong. | Dominant seventh chords | V7 of one particular key | D7-»G | | Major seventh chords | Ima7 of one key or IVma7 of a second key | Gma7-»G, D | | Minor seventh chords | IImi7 of one key, the IIImi7 of a second key or VImi7 of a third key | Ami7-»G, F, C |
The dominant seventh is a very strong pointer to the probable key centre because the V7-»I progression is so common. If that key is one to which all chords belong, then the relationship can be made clearer by writing the chord function for each chord in the best-fit key, that is writing the appropriate Roman numeral for each chord. The tonal effect of different keys can be illustrated by returning to our earlier construct, 'the circle of fifths'. This time we consider not keys but individual notes. In the clockwise direction the notes are each the dominant of the note before while in the anti-clockwise direction each note is the subdominant of the note before. 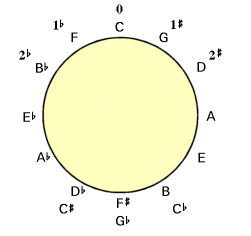 If we consider scales on C, you will see that only the F lies in the descending fifth, subdominant, anti-clockwise direction from C, the key note, while every other note G, D, A, E and B lies in the ascending fifth, 'dominant', clock-wise direction. This predominantly 'dominant' colour is the source of the major scale's strong sense of completeness. This is related to notes that arise from the natural harmonic series. On the other hand, the natural minor scale on C is predominantly 'sub-dominant' with only D and G lying on the 'dominant' side, the remaining notes E flat, F, A flat, B flat lying on the sub-dominant side. The tonic minor chord is less effective as a final chord than its major equivalent which explains the reason why the 'tierce de Picardie', a major chord ending a piece of music in a minor key, became attractive.
|
|
|
Minor Keys
::

|
Key word:
minor keys |
| 1 |
Minor Keys
The same rules can be used to identify minor key centres but so often are the natural minor scale and its harmonies altered to produce more effective melodic and harmonic progressions that relationships become blurred. By substituting a major triad for the minor triad in the Vmi chord (raising the seventh of the natural minor scale by a semitone) or by adding a seventh to give a dominant seventh chord, the 'leading' note is returned to the minor scale. This we have already discussed earlier in lesson10. Find a dominant seventh chord
with a minor chord a tone above | the dominant seventh chord is  VII7 VII7
the minor seventh chord is Imi7 | Find a dominant seventh chord
with a minor seventh chord a fifth below | the dominant seventh chord is V7
the minor seventh chord is Imi7 | | If there is a minor seven flat five chord | it will most often be a IIo chord in the natural minor scale
very occasionally it might be a VIIo in a major key | | If there is a diminished seventh chord | it will often resolve upwards to the tonic, the key note
however, there are exceptions |
In modern music our acceptance of dissonance is far broader than it was say a couple of centuries ago. When Bach harmonised century-old chorales for performance in St. Thomas' in Leipzig, members of the town council attacked him for making the music too dissonant and complex. Today, when we hear the same chorale harmonisations we find it hard to understand what all the fuss was about. So, the sharpened seventh may be used to the accompanying a melody in which the seventh remains unaltered or major/minor chords can be used to add 'spice' to a chord progression.  Before leaving the discussion of chords and minor keys we should take a glance at a special form of the melodic minor scale where the upward scale remains the same when played downward. The sixth and seventh degrees of the scale are not 'flattened' when the scale is played downward. We illustrate the scale, called the 'jazz melodic minor' below. 
|
|
|
Triad Progressions
::

|
Key word:
triads |
| 1 |
Triad Progressions
Triads are nothing like as 'closely' related to keys as chords and, in particular, dominant sevenths. Identifying key centres from triads is really a matter of trial and error. One is trying to find a I chord. Listening to the piece of music should help - almost all music ends on a I chord. Otherwise, place the triads in a particular harmonised scale order and check whether all the triads fit the chosen scale. If any triads do not fit the scale, try again, starting with a different note.
|
|
|
Modes
::

|
Key word:
modes |
| 1 |
Modes
References:
Modes - our introduction to this topic in lesson 25A Brief Introduction to Modes in Early and Traditional European MusicMusic Scales - an excellent summary of the way scales are 'built' and the relationships between them.Second Hand Music - music, noise and silenceGreek Liturgical modesWe have already shown how particular chords can be associated with particular modal scales. One can think of the modal scale as being made up of chord notes infilled with scale notes. If the modal scale is played over its related scale, sometimes one feels a unity between them, such as with the C major scale (also the Ionian modal scale) over the Cma7 chord below.  This is not the case when playing the Ionian modal scale over the Dmi7 chord which you can see and hear below. The scale is based on C while the chord is based on D - two competing key centres  Shifting the scale up a tone to the Dorian mode returns us to a well associated chord and scale.  The point to make clear is that each of these chords and all these scales are actually formed from a single set of seven notes, and yet, some scales feel better with some chords than with others. Each mode has a clear tonal centre.
Modes can be 'associated' with major or minor scales as the chart below shows. A Dorian scale can be thought of as major scale but with lowered 3rd and 7th degrees (scale steps). Similarly, a Mixolydian scale is a major scale but with a lowered 7th degree (scale step).
| major key | key signature | relative minor | Dorian mode | Mixolydian mode |
| C | no sharps/flats | a | d | G |
| G | one sharp (F#) | e | a | D |
| D | two sharps (F#, C#) | b | e | A |
| A | three sharps (F#, C#, G#) | f# | b | E |
| E | four sharps (F#, C#, G#, D#) | c# | f# | B |
| B | five sharps (F#, C#, G#, D#, A#) | g# | c# | F# |
| F# | six sharps (F#, C#, G#, D#, A#, E#) | d# | g# | C# |
| C# | seven sharps (F#, C#, G#, D#, A#, E#, B#) | a# | d# | G# |
| F | one flat (Bb) | d | g | C |
| Bb | two flats (Bb, Eb) | g | c | F |
| Eb | three flats (Bb, Eb, Ab) | c | f | Bb |
| Ab | four flats (Bb, Eb, Ab, Db) | f | bb | Eb |
| Db | five flats (Bb, Eb, Ab, Db, Gb) | bb | eb | Ab |
| Gb | six flats (Bb, Eb, Ab, Db, Gb, Cb) | eb | ab | Db |
| Cb | seven flats (Bb, Eb, Ab, Db, Gb, Cb, Fb) | ab | db | Gb |
Modes offer a rich variety of 'associations' between chords and scales and one should be prepared to experiment to find where certain relationships appear to work well, while others have little or nothing to offer. Music where the chords move too quickly to establish a sense of key can, instead, could use the 'harmonic' associations of scale passages to provide an alternative means of establishing a sense of 'key'. One good example of this is using the C Phrygian mode over a C major triad to give a hint of Spanish flamenco.  The Dorian mode is of particular interest because of its similarity to the natural, melodic and harmonic minor scales. Indeed, one way of identifying that one is dealing with the Dorian mode is that is has a minor 'colour' but with one sharp too many (or one flat too few) in the key signature. We illustrate the four scales below.  Let us now harmonize each scale and number each triad.  The change from a diminished to a minor second 'softens' the II chord making it much more pleasant in chord progressions. Even so, the similarities between the four scales are greater than the differences.
It is worth mentioning at this point that, like the Dorian mode, the Phrygian mode also has a minor 'colour' but appears to have one flat too many (or one sharp too few) in the signature. The Mixolydian mode has a major 'colour' but with one sharp too few (or one flat too many) in the key signature.
Finally, in the table below, we summarise the triads and diatonic seventh chords of the modes, that is those built on each degree of the mode formed of the notes of the mode.
| mode | chord type | I | II | III | IV | V | VI | VII |
| Dorian (Mode I) | triads | i | ii | bIII | IV | v | vi° | bVII |
| Dorian (Mode I) | seventh chords | imi7 | iimi7 | bIIIma7 | IV7 | vmi7 | vimi7b5 | bVIIma7 |
| Phrygian (Mode III) | triads | i | bII | bIII | iv | v° | bVI | bvii |
| Phrygian (Mode III) | seventh chords | imi7 | bIIma7 | bIII7 | ivmi7 | vmi7b5 | bVIma7 | bviimi7 |
| Lydian (mode V) | triads | I | II | iii | #iv° | V | vi | vii |
| Lydian (mode V) | seventh chords | Ima7 | II7 | iiimi7 | #ivmi7b5 | Vma7 | vimi7 | viimi7 |
| Mixolydian (mode VII) | triads | I | ii | iii° | IV | v | vi | bVII |
| Mixolydian (mode VII) | seventh chords | I7 | iimi7 | iiimi7b5 | IVma7 | vmi7 | vimi7 | bVIIma7 |
| Aeolian (natural minor) (mode IX) | triads | i | ii° | bIII | iv | v | bVI | bVII |
| Aeolian (natural minor) (mode IX) | seventh chords | imi7 | iimi7b5 | bIIIma7 | ivmi7 | vmi7 | bVIma7 | bVII7 |
| Ionian (major) (mode XI) | triads | I | ii | iii | IV | V | vi | vii° |
| Ionian (major) (mode XI) | seventh chords | Ima7 | iimi7 | iiimi7 | IVma7 | V7 | vimi7 | viimi7b5 |
| Locrian (mode XIII) | triads | i° | bII | biii | iv | bV | bVI | bvii |
| Locrian (mode XIII) | seventh chords | imi7b5 | bIIma7 | iiimi7 | ivmi7 | bVma7 | bVI7 | bviimi7 |
From the table above, you can read off various triads and seventh chords according to their modal name. For example, the Phrygian II seventh is the flattened supertonic major 7th chord.
In jazz, the association between many common chords and useful scales has been summarised in the table below which is taken from the excellent Jazz Primer by Marc Sabatella.
| chord(s) | scale(s) |
| Cmaj7, Cmaj9, C6, C | C major, C lydian, C major bebop, C major pentatonic, G major pentatonic |
| Cmaj7#11 | C lydian, B in sen |
| Cm7, Cm9, Cm11, Cm | C dorian, C minor bebop, C minor pentatonic, F major pentatonic, Bb major pentatonic, Eb major bebop, C blues, C minor |
| Cm6, Cm | C dorian, C melodic minor, C minor pentatonic, F major pentatonic, Bb major pentatonic, C minor bebop, Eb major bebop, D in sen |
| Cm-maj7 | C melodic minor, C harmonic minor, Eb major bebop |
| Cm7b6 | C minor, Ab major pentatonic |
| Cm7b9 | C phrygian, C phrygian #6 |
| C7, C9, C13, C | C mixolydian, C lydian dominant, C dominant bebop, C blues, C major pentatonic |
| C7sus, Csus, C11, Bb/C, Gm7/C | C mixolydian, C suspended pentatonic, F major pentatonic |
| C7#11, C7 | C lydian dominant |
| C7alt, C7#9#5, C7#9 | C altered, F harmonic minor, F melodic minor |
| C7b9b5, C7b9 | C HW diminished, F harmonic minor, F melodic minor |
| C7aug, C7+, C7#5 | C whole tone |
| Cm7b5 | C locrian #2, C locrian |
| Cdim7 | C WH diminished |
| Cphryg | C phrygian, C phrygian #6, C Spanish phrygian, C in sen |
| Cmaj7#5 | C lydian augmented, C major bebop |
| C7susb9 | C phrygian #6, C phrygian |
|
|
|
Combining Major and Minor Keys
::

|
Key word:
combining major and minor keys |
| 1 |
Combining Major and Minor Keys
The strong association between related major and minor chords makes it difficult to determine at any particular point in which scale a chord is functioning. The minor seventh flat five was identified above as being a VII chord in major keys and a II chord in minor keys. Even the dominant seventh-tonic progression (V-»I) may not be what it seems. The musician that uses his or her ears, will be able to distinguish what on the page appears unclear. So, always play progressions before deciding whether what you think you 'see' is, in fact, what is there!
|
|
|
Modal Interchange
::

|
Key word:
modal interchange |
| 1 |
Modal Interchange
Parallel major and minor keys, e.g. C major and C minor, which share the same key note contrast with relative major and minor keys, e.g. C major and A minor, which share the same key signature. In classical music theory, the diatonic major and minor scales and the harmonies associated with them are called the major and minor modes which should not be confused with the Greek, jazz or church modes, Ionian, Dorian, Phrygian, etc., mentioned in an earlier section. By drawing chords from both related major and minor keys we get what is called Modal Interchange. We can use this idea to analyse chords where the piece is in a major key and minor chords have been 'borrowed' from the parallel minor, Alternatively with a piece in a minor key we may find chords 'borrowed' from the parallel major. Using our ears we can usually distinguish betwen the two cases. If we take C major, chords that do not belong to the C major scale are to be treated as 'alterations'. We also show the scale harmonisation of the Dorian mode. | Scale Step | I | IImi | IIImi | IV | V | VImi | VIIo | | Major Scale | C | Dmi | Emi | F | G | Ami | Bo | | Parallel Natural Minor Scale | Cmi | Do | E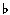 | Fmi | Gmi | A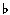 | B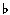 | Natural Minor Chords
numbered in
Major Key Centre | Imi | IIo | 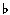 III III | IVmi | Vmi | 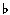 VI VI | 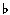 VII VII | | Dorian Scale | Imi | IImi | 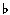 III III | IV | Vmi | VIo | 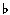 VII VII |
If we now take C minor, chords that do not belong to the C minor scale are to be treated as 'alterations'. We again include the scale harmonisation of the Dorian mode. | Scale Step | Imi | IIo | 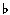 III III | IVmi | Vmi | 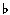 VI VI | 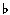 VII VII | | Natural Minor Scale | Cmi | Do | E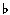 | Fmi | Gmi | A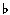 | B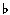 | | Parallel Major Scale | C | Dmi | Emi | F | G | Ami | Bo | Major Chords
numbered in
Natural Minor Key Centre | I | IImi | 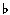 IIImi IIImi | IV | V | 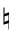 VImi VImi | 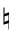 VIIo VIIo | | Dorian Scale | Imi | IImi | 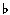 III III | IV | Vmi | VIo | 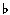 VII VII |
Some of the'altered' chords, that is those 'borrowed' from the parallel scale, are identical to those found in the harmonised Dorian model. Similarly, some of the 'altered' chords occur in the harmonised harmonic minor scale, showing yet again, the similarities between all the minor scales and the Dorian mode. As to which scale one considers the most 'fundamental' and therefore the one upon which all minor key harmonic analysis should be based, different authorities take different positions. Musicians, on the other hand, just need an explanation that helps them play the music, and what we have offered above does do this.
|
|
|
Using Dominants
::

|
Key word:
dominants |
| 1 |
Using Dominants
In diatonic major and minor progressions the dominant seventh provides a strong pointer to the key centre. Some other harmonic 'systems' are not so obliging. The harmonised 'blues' scale has three dominant seventh chords, I, IV and V. Yet, when listening to 'blues' music, there is in no sense a feeling that there are three competing key centres. Rather. the tonic chord provides as strong a sense of key as it does in major or minor keys. One might say that only one of the dominant sevenths is 'true', the others being 'false'. 'True' and 'false' are not a good choice of words because all three are real dominant sevenths satisfying the proper chord formula. A better way of describing them is to look at the 'pull' one feels when these dominant sevenths are played. The V7 chord in the key of the piece will 'pull' us to the tonic, the I chord. This was the chord progression we suggested gives us the best pointer in diatonic harmony to the key centre. The question we have to answer is, 'where do the other dominant sevenths pull us?'  The A7 chord is a dominant seventh pulling us towards the following Dmi chord. The Dmi chord does not signify a new key centre. The key centre remains C major. Therefore we call the A7 a 'secondary dominant', because it is acting as the V7 to a chord, in this case the IImi chord, which is not the tonic chord. Its full functional name is V7/II or 'five seven of two'. Secondary dominants may preceed major and minor keys chords except for the two dissonant diminished chords, VIo in major keys, and IIo in minor keys, neither of which provides an acceptable resolution for the dominant seventh chord. Where a V7 chord does properly anticipate a chord then it is called a 'functioning dominant'. If, however, the harmony is meant to mislead and the chords following are not a proper resolution of the V7 then the dominant seventh is said to be non-functioning. Listen to a progression before deciding which type of V7 one is looking at. A functioning dominant seventh which, because of the dissonant 'tritone' between the major third and minor seventh, wants to resolve to a tonic chord, may be replaced with a dominant seventh chord with its root a diminished fifth, a 'tritone', away. This substitute chord shares the same tritone as the original dominant seventh. This is called 'flat five' or 'tritone' substitution. We illustrate the two progressions below. 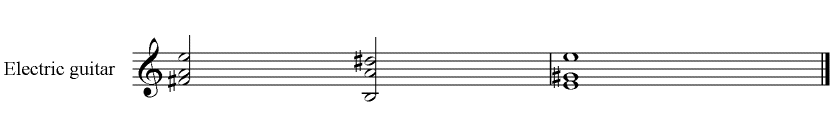 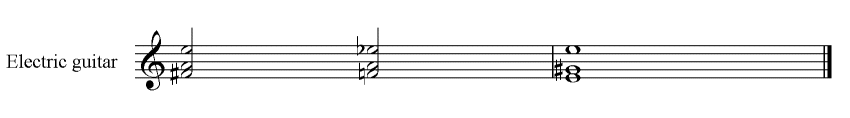 The most obvious change between these two progressions, and in practice the most important, is in the bass line which now becomes a falling chromatic line while the upper notes remain the same. The substitute chord is a flatII7, called a 'flat two seven'. Indeed, all functioning secondary dominants and dominant sevenths in minor keys, that resolve to their tonic, may undergo 'flat five substitution' which leads to the characteristic falling chromatic bassline. The functional names and numbers must show their relationship to the chord to which they resolve, whether the tonic I or the resolution chord of a secondary dominant.
|
|
|
Diminished Seventh Chords
::

|
Key word:
diminished sevenths |
| 1 |
Diminished Seventh Chords
The diminished seventh chord has one particularly interesting property; the interval between successive notes is a minor third. As a result any note may be the root and the chord then have four different names. Within the diatonic system, the diminished seventh in the VIIo7 chord. Outside a diatonic setting, the chords structure allows it to function in many other ways, two of which we describe below.  In the first both the first inversion V7 and the root position VIIo7 chords resolve to the tonic I chord. While the diminished seventh chord exists within the harmonic minor scale, it can also be used in a major key setting and it is said then to be 'substituting' for the dominant seventh. Whichever of the four notes lies in the bass, the diminished seventh, will successfully substitute for the dominant seventh because in all four variants the leading note is present and it is this that 'resolves' by moving to the tonic in the final I chord. Dominant seventh substitution can also occur when the dominant seventh chord is acting as a secondary dominant. 
We thank Adrian Drover for pointing out errors in an earlier version of this example.
In the key of C major, the two diminished seventh chords are acting as secondary dominant seventh substitutes to the minor chords of D, II and E, III. For this reason the functional numbering becomes VIIo7/II and VIIo7/III respectively and their names are 'seven diminished of two' and 'seven diminished of three'. In both cases one of the notes of the diminished chord will be the leading note of the chord that follows it. If none of the notes of the diminished chord is the leading note of the chord following the diminished seventh functions as a passing chord and not as a dominant substitute.
|
|
|
Melodic Substitution
::

|
Key word:
melodic substitution |
| 1 |
Melodic Substitution
Just as harmonies can be substituted below diatonic melodies, so melodies can be modified so that they mirror the substitute 'altered' chords which do not 'properly' fit the harmonised key centre scale. This option increases the opportunities available to the improviser.
|
|
|
Reharmonisation
::

|
Key word:
melodic substitution |
| 1 |
Reharmonisation
Chordal and melodic substitution is met so often in modern popular music that one needs a clear understanding of how to number them and of how to identify their function. When chords in a progression are replaced by alternatives from the same harmonised scale, the procedure is called 'diatonic substitution' and the whole exchange process is called 'reharmonisation'. The substitution entails replacing a chord with a particular function with another chord that has the same function. We summarise the chord family relationships below. | Chord | Family | Role or Purpose | | I | tonic family | temporary or permanent resting chord | | IImi | subdominant family in major keys | move away from tonic | | IIo | subdominant family in minor keys
first inversion flatVII triad often replaces IIo | move away from tonic | | flatIII | tonic family in minor keys | temporary or permanent resting chord | | IIImi | tonic family in major keys | temporary or permanent resting chord | | IVmi | subdominant family in minor keys | move away from tonic | | IV | subdominant family in major keys | move away from tonic | | Vmi | dominant family in minor keys | move towards tonic | | V | dominant family in major keys
also in raised 7th minor keys | move towards tonic | | flatVI | tonic family in minor keys | temporary or permanent resting chord | | VImi | tonic family in major keys | temporary or permanent resting chord | | flatVII | dominant family in minor keys | move towards tonic | | VIIo | dominant family in major keys
also in raised 7th minor keys
first inversion V triad often replaces VIIo | move towards tonic |
|
|
|
Modulation
::

|
Key word:
modulation |
| 1 |
Modulation
We have spent a lot of time trying to show how exotic chord changes, during which there is no real sense that the key centre has shifted, can be correctly numbered or named. Even so, there are times when the key centre does change and this we call modulation. Three types of modulation are given special names.
| Parallel or Parallel Key Modulation | change of key from one key to another where the key note remains the same
(e.g. A minor to A major, or E major to E minor) |
| Relative or Relative Key Modulation | change of key from one key to another where the key signature remains the same
(e.g. A minor to C major, or G major to E minor) |
| Enharmonic Modulation | where there is no audible change of key (at least not in equal temperament) but a chord is rewritten using enharmonic equivalents. There are two main types of enharmonic modulations: dominant seventh/augmented sixth, and diminished seventh. By respelling the notes, any dominant seventh can be reinterpreted as a German or Italian sixth (depending on whether or not the fifth is present), and any diminished seventh chord can be respelled in multiple other ways to form other diminished seventh chords |
The chord naming convention expects that up to the point of modulation all chords will be numbered in relation to the original key centre, but that from the point of modulation, the chords will be numbered in relation to the new key centre. For the practical musician, the question is, when and where does modulation take place. In some pieces the change can be from chord to chord, what is called direct modulation. In other cases, the music might pass through a chord that is common to both keys, the chord acting as a link or pivot. Unsurprisingly, this is called pivot chord modulation. There is no need to change the key signature when a piece modulates, although this can sometimes happen. However, it is not unusual in a piece where there has been a change of key, to find it modulate back to its original key so ending in the same key as it began. Walter Piston's analysis of what used to be called transient modulation demonstrates that modulation over a very short period might be better described in another way. To summarise:
| Phrase Modulation | phrase modulation is a change of key centre at the juncture of two phrases, so that the first phrase ends in one key, and the next phrase begins in another |
| Static Modulation | in static modulation the key centre can change anywhere, not just between two phrases. |
Pivot Chord Modulation or
Common Chord Modulation | when a chord functions diatonically in two different keys and this property is exploited so that before the chord the piece is in one key and after the chord the piece is in another, this is pivot chord or common chord modulation |
| Common Note Modulation | a sustained or repeated pitch from the old key acts as a bridge between it and the new key. Usually, this pitch will be held alone before the music continues in the new key. For example, a held F from a section in Bb major could be used to transition to F major |
Sequential Modulation or
Rosalia | where during a sequence several keys might be visited for one or two beats at a time, such is an example of sequential modulation |
| Transient modulation | the concept of the secondary dominant was not recognized in writings on music theory prior to 1939. Before this time, in music of Bach, Mozart, Beethoven, and Brahms, a secondary dominant, along with its chord of resolution, was considered to be a modulation. Because the effect of modulation was so short, and did not sound like a real arrival of a new key, the two chords had a special name--"transient modulation"--that is, a modulation in which the new key is not established. Since this was a rather self-contradictory description, theorists in the early 1900s, such as Frank Shepard, Benjamin Cutter, and George Wedge, searched for a better description of the phenomenon. In 1939, in a monograph entitled "Principles of Harmonic Analysis," Walter Piston first used the analysis "V7 of IV." (Notably, Piston's analytical symbol always used the word "of"--e.g. "V7 of IV" rather than the virgule "V7/IV.) In his 1941 "Harmony" Piston used the term "secondary dominant" for the first time. It has been generally accepted into music theory since then
[this entry directly quotes from Secondary dominant] |
| Abrupt or Shift Modulation | a variant of phrase modulation, but applied at the end of a varse in a ballad. The reprise of earlier material is presented in an unrelated, usually at a high pitch, in order to inject some tension. It is not usual after a shift modulation in a ballad for there to be a return to the original key - usually the ballad ends in the higher key |
One measure of the proximity of one key to another when considering modulation is the number of notes their scales have in common. For the scales of C major and the natural minor on a (which have the same notes are are therefore treated as being the same) the relationships may be summarised as follows. Minor keys
on the flat side | Major keys
on the flat side | Number of notes in common
with C major or the natural minor on a | Major keys
on the sharp side | Minor keys
on the sharp side |
| d minor | F major | 6 | G major | e minor | | g minor | B flat major | 5 | D major | b minor | | c minor | E flat major | 4 | A major | f sharp minor | | f minor | A flat major | 3 | E major | c sharp minor | | b flat minor | D flat major | 2 | B major | g sharp minor | | e flat minor | G flat major | 1 | F sharp major | d sharp minor |
Chords use only a few notes from any scale. This allows composers to exploit the intrinsic ambiguity that chords have in that they can function diatonically in more than one key. This offers an effective way of modulating using the pivot chord principle where a single chord can be found in both the key from which one is modulating and in the key to which one wishes to modulate. Parallel major and minor keys (for example, C major and c minor) which have only four notes in common, happen to share a common tonic and dominant chord and seem harmonically more closely related than the measure based on the number of shared notes might lead one to expect. Modulation is easily achieved by using the common dominant chord as a pivot. A further ambiguity arises from the way chords may be written in different keys. Chords can be rewritten enharmonically. For example, the dominant seventh (C-E-G-B flat) can be written as an augmented sixth (C-E-G-A sharp). This modulation is more effective if the fifth is unvoiced in the chord. Another example is the augmented triad (C-E-G sharp) which can be reinterpreted (A flat-C-E) or (E-G sharp-B sharp). A similar enharmonic reinterpretation is available with the diminished seventh chord (C-E flat-G flat-B double flat). This topic is explained more fully in Andrew Milne's web page, part of The Tone Centre, entitled Modulation. For those interested in reading further on this topic we recommend Arnold Schoenberg's Structural Functions of Harmony (first published in 1954).
Though modulation generally refers to changes of key, of course any parameter may be modulated. We describe some common non-harmonic modulations in the table below.
| Metric Modulation | tempo modulation, change in tempo |
| Timbral Modulation | gradual changes in tone color |
| Spatial Modulation | changing the location from which sound occurs |
|
|
|
Alan Belkin's General Principles of Harmony
::

|
Key word:
harmony |
| 1 |
Alan Belkin's General Principles of Harmony
Those wishing to study harmony more extensively may wish to refer to Alan Belkin's General Principles of Harmony
We set out below the contents to his excellent resource via which you can review topics of interest.
Alan Belkin's General Principles of Harmony: Table of Contents :: 
Table of contents
- Why this book
- Discussion of other approaches
- Limits of our discussion
- A new approach to understanding harmony
- Basics
- A definition of harmony
- Intervals
- Chords
- Progressions
- Principles of coherence and continuity
- Pitch and interval limitations
- Linear aspects: melody and bass lines; voice leading
- An aside: open vs. closed harmonic systems
- Hierarchy, landmarks
- Principles of movement, interest and of variety
- General aspects of harmonic accent
- Creating momentum and renewing interest on various structural levels
- Locally
- Higher Levels
- Harmonic rhythm
- Modulation and Harmonic Transition
- Transitions between various types of Harmony
- Harmony and Texture; Orchestration and Harmony
- Spacing and register
- Doubling
- Timbre
- Harmony with multiple planes of tone
- Criteria for evaluating harmony
- Pedagogy
N.B. All this material (text and all musical examples) © Alan Belkin, 2003. It may not be quoted or used without the giving full credit to the author. Legal proof of copyright exists.
|
|
 :: next lesson :: next lesson
| |
 :: next lesson
:: next lesson