|
Degrees of the Scale
::

|
Key words:
tonic
supertonic
mediant
subdominant
dominant
submediant
subtonic
leading note
degree |
| 1 |
Degrees of the Scale
In lesson 8 we first mentioned the degrees of the scale. If we take the major scale of C, the key note C is called the first degree of the scale, D is the second degree of the scale, and so on. If we move to another key note, the note row will be composed of different notes but the relationship between the notes in the row will remain unchanged.
The degrees of the scale have their own names.
|
degree | name | definition |
| 1, i, I | tonic (English)
tonique (French f.)
tonica (Italian f.)
Tonika (German f.)
tónica (Spanish f.) | the key note |
| 2, ii, II | supertonic (English)
sus-tonique (French f.)
sopratonica (Italian f.)
Supertonika (German f.)
supertónica (Spanish f.) | the note above the tonic |
| 3, iii, III | mediant (English)
médiante (French f.)
mediante (Italian f.)
modale (Italian f.)
caratteristica (Italian f.)
Mediante (German f.)
mediante (Spanish f.) | the note between the tonic and dominant above (the middle of a perfect 5th counting up from the tonic) |
| 4, iv, IV | subdominant (English)
sous-dominante (French f.)
sottodominante (Italian f.)
Subdominante (German f.)
subdominate (Spanish f.) | the note a perfect fifth below the tonic |
| 5, v, V | dominant (English)
dominante (French f.)
dominante (Italian f.)
Dominante (German f.)
dominante (Spanish f.) | the note a perfect fifth above tonic |
| 6, vi, VI | submediant (English)
superdominant (English)
sus-dominante (French f.)
sopradominante (Italian f.)
Submediante (German f.)
superdominante (Spanish f.) | the note between the subdominant and tonic (the middle of a perfect 5th counting down from the tonic) |
| 7, vii, VII | leading note (English)
leading tone (US)
(note) sensible (French f.)
(nota) sensibile (Italian f.)
Leitton (German m.)
sensible (Spanish f.)
subtonic (English)
sottotonica (Italian f.)
sous-tonique (French f.)
Subtonika (German f.)
subtónica (Spanish f.) | the note a semitone (half step) or tone (whole step) below the tonic, leads to the tonic. theorists make a distinction between 'leading note' (leading tone) and 'subtonic'. The name subtonic is reserved for the flattened or lowered 'leading note', so that the subtonic is a semitone or half step lower than the leading note (or leading tone) |
| 8, viii, VIII | tonic (English)
tonique (French f.)
tonica (Italian f.)
Tonika (German)
tónica (Spanish f.) | the key note |
The Latin prefixes super-, meaning 'above' and sub-, meaning 'below' feature prominently in the naming of the degrees of the scale. The dominant is a fifth above the tonic while the subdominant is a fifth below the tonic. So, for example, when C is the tonic, a 5th above the tonic is G (dominant) and the note a 5th below the tonic is F. 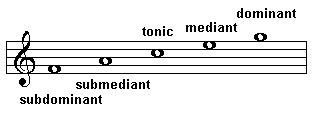 Similarly, for the mediant, except that it is a 3rd above and below the tonic rather than a fifth. The 7th degree of the scale (the Leading Note) is also known as the subtonic, which happens to be a 2nd below the tonic while the supertonic is a 2nd above the tonic.
We set out below the scale degrees for every major key.
|
Scale/Degree
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII (octave)
|
Italian
English
German
French
Spanish
Spanish
|
unisono (m.)
unison
Prime (f.)
unisson (m.)
primera (f.)
primer grado (m.)
|
seconda (f.)
second
Sekunde (f.)
seconde (f.)
segunda (f.)
segundo grado (m.)
|
terza (f.)
third
Terz (f.)
tierce (f.)
tercera (f.)
tercer grado (m.)
|
quarta (f.)
fourth
Quarte (f.)
quarte (f.)
cuarta (f.)
cuarto grado (m.)
|
quinta (f.)
fifth
Quinte (f.)
quinte (f.)
quinta (f.)
quinto grado (m.)
|
sesta (f.)
sixth
Sexte (f.)
sixte (f.)
sexta (f.)
sexto grado (m.)
|
settima (f.)
seventh
Septime (f.)
septième (f.)
séptima (f.)
séptimo grado (m.)
|
ottava (f.)
octave
Oktave (f.)
octave (f.)
octava (f.)
|
|
A
|
A
|
B
|
C#
|
D
|
E
|
F#
|
G#
|
A
|
|
Bb
|
Bb
|
C
|
D
|
Eb
|
F
|
G
|
A
|
Bb
|
|
B
|
B
|
C#
|
D#
|
E
|
F#
|
G#
|
A#
|
B
|
|
Cb
|
Cb
|
Db
|
Eb
|
Fb
|
Gb
|
Ab
|
Bb
|
Cb
|
|
C
|
C
|
D
|
E
|
F
|
G
|
A
|
B
|
C
|
|
C#
|
C#
|
D#
|
E#
|
F#
|
G#
|
A#
|
B#
|
C#
|
|
Db
|
Db
|
Eb
|
F
|
Gb
|
Ab
|
Bb
|
C
|
Db
|
|
D
|
D
|
E
|
F#
|
G
|
A
|
B
|
C#
|
D
|
|
Eb
|
Eb
|
F
|
G
|
Ab
|
Bb
|
C
|
D
|
Eb
|
|
E
|
E
|
F#
|
G#
|
A
|
B
|
C#
|
D#
|
E
|
|
F
|
F
|
G
|
A
|
Bb
|
C
|
D
|
E
|
F
|
|
F#
|
F#
|
G#
|
A#
|
B
|
C#
|
D#
|
F
|
F#
|
|
Gb
|
Gb
|
Ab
|
Bb
|
Cb
|
Db
|
Eb
|
F
|
Gb
|
|
G
|
G
|
A
|
B
|
C
|
D
|
E
|
F#
|
G
|
|
Ab
|
Ab
|
Bb
|
C
|
Db
|
Eb
|
F
|
G
|
Ab
|
|
|
|
Melodic & Harmonic Intervals
::

|
Key words:
melodic interval
harmonic interval |
| 1 |
Melodic & Harmonic Intervals
We could consider the note row in terms of 'intervals' rather than 'degrees'. In a crude sense we have already done this when we found that the major scale is made up of the 'interval' sequence tone-tone-semitone-tone-tone-tone-semitone. What we have not done, however, is consider the interval between the key note and each of the other notes of the scale, whether played in sequence, called a melodic interval or when played as two notes together to produce a harmonic interval. It is important to realise that when we calculate intervals we fix the lower note and vary the upper note. In the case of a melodic interval this is true whether, in the melody, the upper precede the lower note or the lower precedes the upper.
|
|
|
Unisons & Octaves
::

|
Key words:
dyad
unison
octave
perfect unison
perfect prime
augmented unison
augmented prime
diminished unison |
| 1 |
Unisons & Octaves
If we imagine a second note sounding at the same time as the key-note (they form a dyad), we could ask ourselves what is the interval between them? The simplest interval we can consider is the interval between two identical notes - e.g. C and C. The interval is called the unison, the perfect unison or the perfect prime. We can also say that the notes are 'in unison'. The interval from C to C sharp is called the augmented unison or the augmented prime - 'unison' because the note names are the same (both Cs), 'augmented' because the interval is one semitone greater than a 'perfect' unison. The interval from C to C flat is called the diminished unison or the diminished prime Some theorists do not allow the diminished unison because the C flat lies below the C natural and this breaks the rule that all dyadic intervals are named from the lower note. If we now consider the interval between our key-note C and any other C, we would say that the interval is one, two, three or more octaves depending on which C is the upper note; for example, the eighth degree of the scale is one octave above the key-note.
|
|
|
Diatonic Intervals
::

|
Key words:
perfect intervals
major intervals
minor intervals |
| 1 |
Diatonic Intervals
What we call the simple intervals, we illustrate below. In each case the key-note is middle C. On the first line, each degree of an ascending C major scale except the first is placed over the key-note, middle C. We show the names of the intervals below the line. All intervals that are not perfect (the perfect intervals are the unison, fourth, fifth and octave) are called 'major', i.e. forming part of the major scale. In the second line (note the change of key signature) we have set out the harmonic minor scale of C minor above middle C. Only two intervals are different from those on the first line - the third (C to E flat - note the key signature) and the sixth (C to A flat - again, note the key signature). Each of these two upper notes is lower by one semitone than that in the major scale in line 1. For this reason the intervals are said to be 'minor'. Lines 3 and 4 (also with a three flat key signature) are the ascending and descending melodic minor scales. Only the minor seventh is new - the upper note is one semitone lower than that in the major scale - and the interval is said to be 'minor'. The perfect intervals remain unchanged as one moves from the major to either of the minor scales.  To listen to these intervals play the Scorch score below. If the key note is changed and the proper scales, major, harmonic minor and melodic minor, are set out as above, the sequence of intervals would remain the same for each scale. It is the sequence of intervals that characterises the three scales and these are unchanged as the key-note is changed.
|
|
|
Chromatic Intervals
::

|
Key words:
doubly diminished
diminished
augmented
doubly augmented
quality of intervals |
| 1 |
Chromatic Intervals
Dr Alan Crosier offers a succinct definition of a chromatic interval.
|
Diatonic intervals are all those whose notes can both be found in at least one major or harmonic minor scale (example: F and B are both found in C major); all other intervals are chromatic (for example F and B#, since no major or harmonic minor scale whose key note is C includes both of them). |
When we talk about widening or narrowing an interval, we understand that only the degree of inflection is changing - that is, the note name remains the same but the inflection sign changes. We say that the interval is being widened or narrowed chromatically (specifically without changing the note name).
If a major or perfect interval is widened by sharpening chromatically the upper note a further semitone the interval is said to be augmented; if widened again by raising the upper note chromatically a further semitone, the interval is said to be doubly augmented. If a minor or perfect interval is narrowed by flattening chromatically the upper note a further semitone the interval is said to be diminished; if the upper note is flattened chromatically by a further semitone, the interval is said to be doubly diminished. Perfect intervals and major/minor intervals behave slightly differently when 'sharpened' or 'flattened' chromatically as the table below demonstrates.
| | chromatically sharpen one semitone (+ 1/2 tono)- move up | doubly augmented
sur-augmenté (French)
doppelt übermäßig (German)
più che aumentato (Italian)
doble aumentado (Spanish) | | doubly augmented
sur-augmenté (French)
doppelt übermäßig (German)
più che aumentato (Italian)
doble aumentado (Spanish) | augmented
augmenté (French)
übermäßig (German)
eccedente (Italian)
aumentado (Spanish) | augmented
augmenté (French)
übermäßig (German)
eccedente (Italian)
aumentado (Spanish) | major
majeur (French)
groß (German)
maggiore (Italian)
mayor (Spanish) | perfect
parfait (French)
rein (German)
giusta (Italian)
justa (Spanish) | minor
mineur (French)
klein (German)
minore (Italian)
menor (Spanish) | | diminished
diminué (French)
vermindert (German)
diminuito (Italian)
disminuido (Spanish) | diminished
diminué (French)
vermindert (German)
diminuito (Italian)
disminuido (Spanish) | doubly diminished
sous-diminué (French)
doppelt vermindert (German)
più che diminuito (Italian)
doble disminuido (Spanish) | doubly diminished
sous-diminué (French)
doppelt vermindert (German)
più che diminuito (Italian)
doble disminuido (Spanish) | | chromatically flatten one semitone (- 1/2 tono) - move down |
|
The rules for naming intervals are given below.
| intervals are named from note to note, in the key of the lower note, and from the lower note. For example, intervals from C to G double flat, G flat, G, G sharp or G double sharp are all fifths because C to G is a fifth. They are, in order: doubly diminished fifth, diminished fifth, perfect fifth, augmented fifth, doubly augmented fifth. If the G double sharp is written as an A (its enharmonic equivalent) the interval is now a sixth - because the interval C to A is a sixth; in fact it is a major sixth. | | the sequence for perfect intervals (unisons, octaves, fourths and fifths) is doubly diminished - diminished - perfect - augmented - doubly augmented as the interval to the key-note is increasingly widened. | | the sequence for major and minor intervals (seconds, thirds, sixths and sevenths) is doubly diminished - diminished - minor - major - augmented - doubly augmented as the interval to the key-note is increasingly widened. |
It is important to understand that we are talking about the way theorists notate intervals. They are not interested in the 'sound' of the 'interval', only in the way is 'looks' on the page. For example, the interval 'C to G' is a perfect fifth while the interval 'C to A double flat' is a diminished sixth, but to the listener, the two intervals played on a modern piano, sound identical. Many 'intervals' have enharmonic equivalents but, for the sake of consistency, theorists stick to naming rules that distinguish between them. If you 'heard' them without reference to a score, rather than 'read' them from the page, many of the more exotic interval name distinctions would be quite irrelevant. The collective name quality is given to the terms major, minor, augmented, diminished, doubly-augmented, doubly-diminished and perfect.
When describing the quality of an interval, the term 'perfect' refers to intervals that, because of their extremely simple pitch relationships, are possessed of a high degree of consonance. The just fifth is a member of the harmonic series, as is the octave, and the frequency ratios that define the pure fifth (3:2) and the octave (2:1) are very simple. The fourth, which is the complement to the fifth, is also expressed, in terms of frequencies with a similarly simple ratio (4:3). What distinguishes 'perfect' intervals from seconds, thirds, sixths and sevenths is that when a 'perfect interval' is inverted, it remains perfect. Augmented, diminished, major and minor intervals all change their quality under inversion. The very earliest attempts at harmony in Gregorian chant involved only the octave and the fifth. The fourth, although 'perfect' because its quality is invariable under inversion, is considered a stylistic dissonance in certain contexts, namely in two-voice textures and whenever it appears above the bass.
|
|
|
The Tritone
::

|
Key words:
tritone
diabolus in musica
consonance by circumstance |
| 1 |
The Tritone
Before passing on to compound intervals, we should examine one particular interval called the tritone, an interval made up of three whole tones (six semitones), the only interval that is the same as its inverse. In early music theory this interval was avoided. The entry for "tritone" in the New Grove Dictionary of Music and Musicians traces the tradition of this interval as the "devil in music" (diabolus in musica) to mediaeval times and J. J. Fux (1725), in his famous counterpoint treatise Gradus ad Parnassum, gives the traditional rule (Mi contra fa est diabolus in musica) that prohibits singing a pitch needing the solmization syllable mi against one needing the syllable fa. So, the pitches E and F could not be sounded together; neither could E and B flat. However, the story is more complicated. In 1357, Johannes Boen classified the tritone as a consonantia per accidens, i.e. a 'consonance by circumstance'. Specifically, he finds either the tritone or the diminished fourth acceptable when the former is accompanied by a lower minor third, e.g. e-g-c# (minor 3rd + tritone), or the latter is accompanied by a major third, e.g. d-f#-b flat (major 3rd + diminished 4th). The perfect fourth is likewise in this category of "situational consonance" (to use a modern expression) when accompanied by an octave and lower fifth, e.g. d-a-d'. Reference:
Tritones in early music: Were they always prohibited? by Margo Schulter.The summary above is drawn from her article.
|
|
|
Compound Intervals
::

|
Key word:
compound interval |
| 1 |
Compound Intervals
Intervals continue beyond the octave. They are named 9th, 10th, 11th, 12th and so on. Intervals beyond the octave are called compound intervals. A major 12th, which is an octave plus a fifth can be called a 'compound perfect 5th'. Note that because the octave note is included in both intervals, the intervals do not obey the rules of arithmetical addition. Normal arithmetic tells us that 8 + 5 = 13 but the arithmetic of intervals shows us that 8ve + 5th = 12th. This is because the note at the top of the 8ve is repeated as the note at the bottom of the 5th. We only need to include it once in the compound interval of a 12th. Compound intervals can have all the qualities (diminished, minor, major, augmented, perfect) we have already met with smaller intervals. | Combine | Compound Interval | Comment | | 8ve plus 2nd (octave plus second) | 9th | not in triad - see extended chords | | 8ve plus 3rd (octave plus third) | 10th | harmonically like a 3rd of a triad | | 8ve plus 4th (octave plus fourth) | 11th | not in triad - see extended chords | | 8ve plus 5th (octave plus fifth) | 12th | harmonically like a 5th of a triad | | 8ve plus 6th (octave plus sixth) | 13th | not in triad - see extended chords | | 8ve plus 7th (octave plus seventh) | 14th | harmonically like a 7th - see sevenths and seventh chords |
Intervals beyond the thirteenth are of use only to theorists.
|
|
|
Table of Intervals
::

|
Key word:
table of common intervals |
| 1 |
Table of Intervals
The following table lists the names of the most common intervals by number of semitones (half steps) in the interval. The quality of the intervals is shown by P for perfect, M for major, m for minor, d for diminished and A for augmented.
| Interval in semitones | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Interval | P1 or PU | m2 | M2 | m3 | M3 | P4 | d5 | P5 | m6 | M6 | m7 | M7 | P8 | m9 | M9 | m10 | M10 |
Interval
(alternative descriptor) | d2 | A1 | d3 | A2 | d4 | A3 | A4 | d6 | A5 | d7 | A6 | d8 | A7 | A8 | d10 | A9 | d11 |
You should remember that diminished intervals are often notated using chord tokens, namely d, dim. or o. Augmented intervals, too, have their own chord tokens, A, Aug. or +.
Everything written above is fine when one is using scales based on 12 divisions of the octave, a scale built on combinations of tones (whole steps) and semitones (half-steps). The common Western musical scales are of this type. If you want to notate scales with a greater number of divisions and incorporating microtones, the naming protocol becomes very complicated. This problem is discussed in the two references given below.
References:
The Musical Intervals Tutor
|
|
 :: next lesson :: next lesson
| |
 :: next lesson
:: next lesson
