|
Origin of Diatonic and Chromatic Scales
::
|
Key words:
monochord
Pythagoras
interval
lyre |
| 1 |
Origin of Diatonic and Chromatic Scales
We owe the concept of scale and temperament to the ancient Greeks. About the origin of the diatonic scale, the ancient Greek music theoretician, Aristoxenus of Tarantum (fourth century B.C.), wrote: "We can establish that the diatonic is the first (proton) and the oldest (presbyteron); this is the type that the human voice naturally finds" (Harmonic Elements I, cited by Haik-Vantoura in her Les 150 Psaumes dans leurs melodies antiques, p. T-51). The chromatic scale, which may be derived from the diatonic scale, was also ancient. Aristoxenus' view is that its origins "go back into the night of time". He also cited "mixed" scales of the "diatonic-chromatic" genre (a modern example being our "harmonic minor"), as did Plutarch (46-127), Greek historian, biographer, essayist, supposed author of De musica, (taken from Plutarch's Moralia). Many of these ideas may indeed have originated with the Babylonians. This topic is covered in much greater detail in the thesis referenced below. The Greeks studied the relationship between string length and pitch with an instrument called the monochord. Its base was a resonating box, over which stretched a single string. With one end secured by a hitch pin, the string passed over a fixed bar or nut, across a moveable bridge, over a second fixed bar, finally secured at its other end by an adjustable tuning peg. Using the moveable bridge to divide the string into two lengths set to different ratios, they could study the relationship between string lengths and interval.  We are taught that Pythagoras (born on Samos in 582 BC) first demonstrated that two strings, the ratio of their lengths being 2:1, produced an interval of an octave and that the shorter string produced the higher note. There is no written evidence from Pythagoras himself and some, including Walter Burkert in his Weisheit und Wissenschaft: Studien zu Pythagoras, Philolaus und Platon (1965) which has been revised and translated into English as Lore and Science in Ancient Pythagoreanism (1972), have seriously undermined Pythagoras' claim (admittedly made by others) to primacy in this field. The earliest documented use of the monochord in this way was by Euclid in about 300 BC. Pythagoras may also have discovered that the interval of a perfect fifth was associated with the ratio 3:2, and that the octave could be completed with a second complementary interval, a perfect fourth, associated with the ratio 4:3. He demonstrated this by multiplying 3:2 by 4:3 giving 2:1, the ratio for an octave. This system was extended by introducing a tone, the difference between a perfect fifth and a perfect fourth, with the ratio 9:8. Using the fact that a perfect fourth is made up of two tones plus one semitone, the ratio for the semitone was calculated to be 256:243. Unfortunately, in order to use these intervals as the basis for building a musical scale, we have to solve the problem that arises from two semitones, each set to the ratio 256:243, not quite making a tone set with the ratio 9:8. The association of musical harmony with ratios of small integers would have commended itself to early Greek philosopher-mathematicians who believed that all numbers were either integer or rational (i.e. a rational number can be written as the ratio of two integers) until it was proved that the square root of two is irrational. The shock was all the greater because one can construct a line of irrational length. The square root of two is the length of the hypotenuse of a right-angled triangle whose other sides are each of unit length. What we know of Greek music indicates that the lyre was one of their most important instruments. There is little evidence that it performed a harmonic role; rather, it seems to have been used to play melody - indeed Ancient Greek music appears to have formed part of an indisoluble complex of poetic texts, accompanying melody and later, in choral lyric poetry, dance.
The early lyre had three strings but, by the seventh century BC, a fourth string had been added. The four strings were most probably tuned to the notes of an ancient Greek Dorian tetrachord (successive descending intervals: tone, tone, semitone), the four notes encompassing a perfect fourth. Relying on vague, even contradictory evidence, we could continue to believe that Pythagoras, or Lichaon of Samos, increased the number of strings to eight, joining two tetrachords with a tone between them to produce what today we call the major scale (intervals: [tone, tone, semitone], tone, [tone, tone, semitone]), the top and bottom strings being one octave apart. This eight-stringed instrument may be what the Greeks called the kithara, from which we get the words 'cittern' and 'guitar'. However, other strong evidence suggests that the Ionian mode that we use today was first proposed in about 1547 by Heinrich Glarean. Reference:
Terpander: The Invention of Music in the Orientalizing Period - by John Curtis Franklin
|
|
|
Modes
::
|
Key word:
mode |
| 1 |
Modes
At the outset it should be stressed that we have no evidence that the 'modes' we discuss below were actually used by the ancient Greeks. All we can be certain is that the modes below stem from the work of a number of medieval musical theorists. We do know that these theorists thought they were rediscovering the work of the ancient Greeks but in many important details they seriously misunderstood what the ancient Greeks or later commentators had written on this subject. In particular, the ancient Greeks analysed their tetrachords on the basis that they were descending note rows while the medieval theorists thought the note rows were ascending. For this reason, it is a mistake to think of modes, as we discuss them below, as being constructs of the ancient Greek when in fact they are really those of medieval theorists.  The history of the system of modes can be traced to the Byzantine system of echoi. Today we apply the term 'mode' to fourteen different 'scales'. The first eight were established during the medieval era to help classify existing Gregorian chants. These are the so-called Church, Gregorian, Ethnic or Ecclesiastical modes. A further four were added in 1547 by the Swiss humanist and scholar Heinrich Loris. Henricus Glareanus, as he was called by his Latin name, spent about 20 years planning his Dodecachordon, and it was completed by 1539, eight years before publication.
Much later, two more were added for completeness. Today, modes have given way to our major-minor system of tonality. Modes come in pairs, authentic and plagal, terms that describe the position in the scale of a particular note, called the finalis or final. When the final is the lowest note in the scale, the scale is said to be authentic. When the final is the fourth note in the scale, the mode is said to be plagal and its name is preceded by the prefix hypo, meaning 'under'. The final is shown below in blue The modal scales set out below use only the white keys on the piano. Each starts on a different degree of the scale. The original eight (protus, deuterus, tritus and tetrardus, in each case either authentic or plagal), where we highlight the tenor, repercussio or reciting tone (marked in red), together with the four of Glareanus are set out with their characteristic sequence of intervals S = semitone and T = tone:
Church, Gregorian or Ecclesiastical Modes set out in the late ninth-century text ALIA MUSICA which mis-applied original Greek names
|
| I | Dorian: authentic : protus authenticus | D E F G A B C D : minor mode | TSTTTST |
| II | Hypodorian: plagal : protus plagalis | A B C D E F G A | | | III | Phrygian: authentic : deuterus authenticus | E F G A B C D E : minor mode | STTTSTT | | IV | Hypophrygian: plagal : deuterus plagalis | B C D E F G A B | | | V | Lydian: authentic : tritus authenticus | F G A B C D E F | TTTSTTS | | VI | Hypolydian: plagal : tritus plagalis | C D E F G A B C | | | VII | Mixolydian: authentic : tetrardus authenticus | G A B C D E F G | TTSTTST | | VIII | Hypomixolydian: plagal : tetrardus plagalis | D E F G A B C D | | Modes introduced in the sixteenth century by Swiss theorist Glareanus (1488-1563)
| | IX | Aeolian: authentic | A B C D E F G A : minor mode | TSTTSTT | | X | Hypoaeolian: plagal | E F G A B C D E | | | XI | Ionian: authentic | C D E F G A B C | TTSTTTS | | XII | Hypoionian: plagal | G A B C D E F G | | Originally rejected by Glareanus because it lacked a perfect fifth above and a perfect fourth below
| | XIII | Locrian: authentic
also called Hyperaeolian | B C D E F G A B : minor mode | STTSTTT | | XIV | Hypolocrian: plagal | F G A B C D E F | |
The tenor is a fifth above the final in the authentic modes and a third below the tenor in the authentic mode when placed in the plagal mode; except when the tenor would have been the note B it is raised to C. The Dorian, Phrygian, Aeolian and Locrian modes are minor modes because in each case the interval between the first and third degree is a minor third. All these modal scales are in effect the same sequence but starting from different notes. The 'colour' of each mode is determined by its sequence of intervals, whole- and half-steps, tones and semitones. Modes are pitch-insensitive; in other words, although our examples have been based on the white notes on a piano, modes can start from any note. What is important is that the required sequence of tones and semitones be preserved in each mode.
Richard Lindsey, writing in the Talkbass forum, makes the following observation:
|
One thing to remember about using the "degrees of the major scale" approach to derive modes is that although you can and do derive the modes that way, modes are also in a way tonalities/modalities of their own. They don't 'necessarily' always have any connection to the major tonality that provides the 'source scale'. Thus, you can have a piece that is in D dorian. The student might be tempted to think, well, doesn't that mean it's really in C major, since D dorian is the second mode of C major. But the answer is no. D dorian, as a tonal centre, is different from the key of C major, even though the D dorian mode has the same component notes as a C major scale. You're probably familiar with the famous Miles Davis tune So What. The harmony is basically D dorian/Eb dorian/D dorian. Not, it is important to note, C major/Db major/C major. Much rock, folk, and ethnic music is actually more modal than it is strictly major/minor. |
Historically, the scale or mode was generally the full range of a chant. There are examples where an extra note above or below the scale was added, and even where chants include notes not in the tone row of a particular mode, what today we would call 'accidentals'. Like so many 'rules' in music theory, there is some disparity between theory and practice.
For example most of the chants of the Divine Office do not fit into the system we have set out above. Scholars were obliged to make a few adjustments to their system. The Antiphonale Monasticum (containing the psalms and a number of short antiphons for monastical use) shows how the system was adapted.
We have taken this table from Gregorian chant - The Music.
| church tone number | name | finalis | tenor |
| I | protus authenticus | D |
A |
| II | protus plagalis | D | F |
| III | deuterus authenticus | E | C |
| III | tonus recentior | E | C |
| IV | deuterus plagalis | E | A |
| IV | tonus alteratus | A | D |
| V | tritus authenticus | F | C |
| VI | tritus plagalis | F | A |
| VII | tetrardus authenticus | G | D |
| VIII | tetrardus plagalis | G | C |
| -- | tonus peregrinus | G | A + G |
| -- | tonus irregularis | A | A |
| -- | tonus in directum | C | C |
The association of particular Greek names with particular modes appears to have taken place during the medieval period. Certainly Boethius (c.480- c.524) associated names differently to each scale. Most modern modal theory, however, uses the names we have given in the chart above. The Ionian mode has become our major scale and the Aeolian mode our natural (or pure) minor scale. For those interested in when the modal system gave way to our modern major-minor key system, we recommend the article entitled When did modal music give way to the modern key system?. The series of fourteen modes can be found for any 'key'. The examples above are all based on the key of C and are derived from the C major scale: C D E F G A B C. By modulating to another key, say D major, the modes will now be various sequences based on the scale of D major: D E F# G A B C# D. Each mode will start on its own degree of the scale; so for example, the authentic form of the Locrian mode will start on the seventh degree (C#) and the sequence will be: C# D E F# G A B C#.
The modes above have been derived from major scales. When using the melodic or harmonic minor scales as the basis for a sequence of modes, the results will be somewhat different because the successive interval sequences are now different. The names of the modes we find for each degree of the scale also change. Let us consider modes formed when the basic scale is the harmonic minor. Here S = semitone, T = tone, and U = three semitones: | Modes based on the C Harmonic Minor scale | | Dorian b2 b5 (or Locrian #6, Locrian #13): | D Eb F G Ab B C D | STTSUST | | Ionian Augmented: | Eb F G Ab B C D Eb | TTSUSTS | | Lydian Minor (or Spanish Phrygian, Dorian #11): | F G Ab B C D Eb F | TSUSTST | | Mixolydian b6 b9 (or Double Harmonic Major, Phrygian #3, Andalusian mode, Oriental mode): | G Ab B C D Eb F G | SUSTSTT | | Aeolian Harmonic (or Lydian #2, Lydian #9): | Ab B C D Eb F G Ab | USTSTTS | | Superlocrian Diminished (or Superlocrian bb7): | B C D Eb F G Ab B | STSTTSU | | C Harmonic Minor: | C D Eb F G Ab B C | TSTTSUS |
Our thanks to Ari Dibyantara for correcting an error in an earlier version of this table.
The modal names have precise meanings. For example, the mode on the second degree of the minor harmonic scale, the Dorian b2 b5, is similar to the Dorian mode in the major scale that carries the same root, where the second (2b) and the fifth degrees (5b) are lowered by a semitone (half-step). The Superlocrian (sometimes written Super-locrian) is a Locrian mode where the 4th has been flattened. It is identical to the 4th mode of the Lydian Dominant scale. The name Lydian Dominant is given to a scale containing the notes of a dominant seventh chord plus a raised fourth - this last is a characteristic of the Lydian mode. The raised fourth is actually the only difference between this scale and the Mixolydian mode. The raised fourth is less dissonant than the natural fourth when played over an ordinary dominant seventh chord. For this reason the Lydian Dominant scale is often preferred to the Mixolydian mode when played over any dominant seventh chord, unless the natural fourth is explicitly specified, as in a sus chord. The Lydian Dominant scale is always preferred if the raised fourth is explicitly specified, for example in a dominant seventh sharp eleven chord. The raised fourth is enharmonic with the lowered fifth; for this reason this chord may be notated 7b5 rather than 7#11. However, the notation 7b5 is often reserved to indicate a different scale, such as the diminished scale or the whole tone scale. The sound of the raised fourth - or, enharmonically, the flat fifth, which is how most musicians refer to it - is characteristic of bebop (about which see bebop below). Unfortunately, once one begins 'naming' modes with altered notes, for example when establishing the modes derived from minor scales, one finds a bewildering choice of names for any particular sequence of notes. The names we have given to the sequences immediately above and below are suggestions only. You should be aware that other writers may use other names. Happily, the sequences themselves do not change, nor the chords that will be associated with them. When the scale is the ascending melodic minor scale the modes are as follows. | Modes based on the ascending C Melodic Minor scale | | Dorian b2 (or Phrygian #6): | D Eb F G A B C D | STTTTST | | Lydian Augmented: | Eb F G A B C D Eb | TTTTSTS | | Lydian b7 (or Lydian Dominant, Acoustic mode, Bartok mode): | F G A B C D Eb F | TTTSTST | | Mixolydian b6 (or Mixolydian b13): | G A B C D Eb F G | TTSTSTT | | Aeolian b5 (or Locrian #2, Lydian #9, Half-Diminished): | A B C D Eb F G A | TSTSTTT | | Superlocrian (or Altered Dominant, Diminished Whole-tone): | B C D Eb F G A B | STSTTTT | | C Melodic Minor: | C D Eb F G A B C | TSTTTTS |
Later we will look at some of the ways practical musicians tried to bend the science of 'natural' scales to reality. It is worth pointing out, however, that music did not have to wait for science in order to become a significant preoccupation of communities around the globe and that, in many parts of the world, scales far more complicated than the 12 semitone scale have been readily adopted, including the use of quarter tones and other microtonal intervals. The Greeks could tune and play the lyre many centuries before the birth of Christ but the mathematical solution to the problem of the vibrating string was not published until 1759, by J. L Lagrange (1736-1813). Modes can start on any note of the major scale starting on any key-note so long as the sequence of intervals between the succeeding notes preserves that which is the source of each mode's 'colour'. The formula for writing modes set out below. | Find the major scale upon which the mode is to be constructed | | G Lydian, for example, is constructed on the fourth degree of the scale of D major, i.e. starts on G; 'colour' is Lydian | | The mode is written with the same key signature as the major scale from which it is derived | | G Lydian, for example, is written with the key signature of D major i.e. two sharps |
If one builds all the modes from the same keynote C the results are as follows: | Mode name | Notes | Scale pattern | Key signature | Major/Minor scale description| Ionian: | C D E F G A B | 1 2 3 4 5 6 7 | | major scale | | Dorian: | C D Eb F G A Bb | 1 2 b3 4 5 6 b7 | Bb Eb | natural minor scale with a raised sixth | | Phrygian: | C Db Eb F G Ab Bb | 1 b2 b3 4 5 b6 b7 | Bb Eb Ab Db | natural minor scale with a lowered second | | Lydian: | C D E F# G A B | 1 2 3 #4 5 6 7 | F# | major scale with a raised fourth | | Mixolydian: | C D E F G A Bb | 1 2 3 4 5 6 b7 | Bb | major scale with a lowered seventh | | Aeolian: | C D Eb F G Ab Bb | 1 2 b3 4 5 b6 b7 | Bb Eb Ab | natural minor scale | | Locrian: | C Db Eb F Gb Ab Bb | 1 b2 b3 4 b5 b6 b7 | Bb Eb Ab Db Gb | natural minor scale with lowered second and fifth
sometimes called 'half diminished' | |
The significance of modes in music lies both in their harmonic and melodic character. The C major scale, for example, contains the four notes of the C major 7th chord - the notes C, E, G, B natural - as well as the four notes of the D minor 7th - the notes D, F, A, C. The modes are each related to particular chords. | Mode Name | Grouped according to sound (also other suggested chords) | | Ionian: | Tonic Major Seventh : Ima7 (also: C, C6/9, C6) | | Lydian: | Subdominant Major Seventh : IVma7 (also: C6/9, D/C, G/C) | | Dorian: | Supertonic Minor Seventh : IImi7 (also: Cmin, Cmin6) | | Phrygian: | Mediant Minor Seventh : IIImi7 (also: Cmin, Db/C, Ab/C, Bbmin/C) | | Aeolian: | Submediant Minor Seventh : VImi7 (also: Cmin, Ab/C, Fmin/C) | | Mixolydian: | Dominant Seventh : V7 (also: C13, Csus4, Bb/C, F/C, Gmin/C) | | Locrian: | Minor Seventh Flat Five : VIImi7(flat 5) (also: Gb/C, Db/C ) |
Because the same chords may occur in different modes and keys, thinking 'modally' gives the improviser scope to use different modal patterns over common chords each with a different key centre but each pattern related harmonically to the same chord. This is a powerful influence on much modern popular music and takes the composer beyond the more limited world of diatonic major and minor scales. The player may want to sharpen or flatten notes in a major scale to give a more 'modal' feel to a sequence, as for example in the Lydian dominant, which we met earlier, - or the Lydian flat seven as it is sometime named. 
The minor scale-mode chord associations are as follows: | Mode Name | Grouped according to sound | | Hypoionian: | Tonic Minor Seventh : Imi7 | | Dorian 2b 5b: | Supertonic Minor Seventh Flat 5 : IImi7 (flat 5) | | Dorian 2b: | Supertonic Minor Seventh: IImi7 | | Ionian augmented: | Mediant Major Seventh Sharp 5 : IIIm7 (sharp 5) | | Lydian augmented: | Mediant Major Seventh Sharp 5 : IIIm7 (sharp 5) | | Lydian minor: | Subdominant Minor Major Seventh : IVmi7 | | Lydian 7b: | Subdominant Major Minor Seventh : IVmi7 | | Mixolydian 6b 9b: | Dominant Seventh : V7 | | Mixolydian 6b: | Dominant Seventh : V7 | | Aeolian harmonic: | Submediant Major Seventh : VIm7 | | Aeolian 5b: | Submediant Minor Seventh Flat 5 : VIm7 (flat 5) | | Superlocrian diminished: | Diminished Seventh : VII dim | | Superlocrian: | Minor Seventh Flat 5 : VIIm7 (flat 5) |
Philippe Varlet (philvan@erols.com) writes some interesting remarks about the role of Scales in Irish folk music: The most common scales are major and minor. One starts with a major 3rd (D to F# for instance), the other with a minor 3rd (D to F natural). These scales are made of whole- and half-steps, with in particular a 1/2 step between the 7th note (called "leading tone/note") and the tonic or "home note." For instance, D major: | Note: | D | | E | | F# | | G | | A | | B | | C# | | D | | interval: | | whole | | whole | | half | | whole | | whole | | whole | | half | |
In Irish instrumental music, the minor scale is very rare, the major scale is the most common. However, Irish tunes are also built on modes of the major scale. The modes are given Greek names in reference to old Greek and medieval music theory, but are also called mode 1, 2, 5, 6 (these are the ones found in Irish music) depending on which note of the major scale they start on. For instance, using the D major scale: | Modes commonly found in Irish Folk Music | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | | Major (Ionian, mode 1): | D | E | F# | G | A | B | C# | | | | | | Dorian (mode 2): | | E | F# | G | A | B | C# | D | | | | | | Mixolydian (mode 5): | | | | | A | B | C# | D | E | F# | G | | | Aeolian (mode 6): | | | | | | B | C# | D | E | F# | G | A |
The Dorian and Aeolian modes sound minor because they start with a minor 3rd, like the minor scale; however, they do not have a leading tone/note. The Dorian mode is by far the more common of the two. If you hear an Irish tune that sounds minor, it is likely to be in Dorian. To make sure, listen to the 6th note: it is a 1/2 step (semitone) higher in Dorian than it is in Aeolian. For instance, E Dorian (see above) has C#, while E Aeolian would have all the same notes except for C natural. The Mixolydian mode sounds major, but also doesn't have a leading tone/note. Sometimes, it is described as having a flat 7th note, because it is a 1/2 step (semitone) lower than a leading tone/note would be in the major scale. Another important characteristic of how these modes are used are their harmonic implications. That is, the tunes are built around certain chords, and these sets of chords vary with each mode. Major (mode 1) tunes are usually built primarily around the I-IV-V chords, the three major chords of any given major key. In D Major for instance, the chords would be D Maj, G Maj, and A Maj. Tunes in other modes are typically built around two chords only, which are a step (one tone) apart. Dorian and Aeolian (modes 2 and 6) will have a minor "home" chord and a major "contrast" chord a step below. Mixolydian (mode 5) tunes will have two major chords. For instance, for modes of the D Major scale: | E Dorian: | E minor and D Major | | A Mixolydian: | A Major and G Major | | B Aeolian: | B minor and A Major |
This is a very basic scheme, but it's a good start for an accompanist who has never heard a tune before and who can spot these chords and build from there.
In his Music Theory for Diatonic Accordion Players Orest Kozulich discusses the use of modes in folk music and the problems performers meet when playing on diatonic accordions.
The particular use made of modes in Irish folk music is mirrored in the folk music of other countries. For example, the Phrygian mode is quite common in flamenco music and is often referred to as the 'Spanish' mode. Composers turn to it when they want to impart to a piece an oriental character. In the hands of a highly skilled composer such as Claude Debussy, the use of modes produces enormous excitement and colour. The movement Fêtes from his orchestral suite Noctures uses Dorian, Lydian and Mixolydian modes. We have set out the score using the 'sound heard' convention so that transposing parts (e.g. clarinets, brass) are shown as heard rather than as originally written.
Reference: George Miller discusses modes
|
|
|
Jazz Scale
::
|
Key word:
jazz scales |
| 1 |
Jazz Scale
The jazz scales can be thought of in the same way as modes: a set of scales starting on different degrees of an underlying scale that use only the notes of that scale. Several commentators object to this approach. They argue that jazz scales are just 'altered' scales and the suggestion that the various scales are related to a single Ur-scale leads to a serious misunderstanding of the way scales are used in jazz and, more importantly, of how jazz musicians actually think about their use. We are sympathetic to this view but many other commentators take a different view on this and so, in a spirit of completeness, we offer the summary below.
The 'standard' Church modes may be thought of as having been derived from an underlying Ionian or major scale. In a similar way, jazz scales can be thought of as having been derived from an ascending melodic minor scale which can be thought of also as a rising major scale but with the third degree lowered (or flattened). As with the 'standard' modes, each scale starts on a different degree of the ascending melodic minor scale. Unlike the 'classical' melodic minor scale, the jazz scales (and modes) remains the same when played up or down. We met jazz scales earlier when discussing the modes based on the melodic minor scale but we show them again.
| Jazz Scales based on the C Melodic Minor |
| D Dorian 2b (Dorian Flat 2): | D Eb F G A B C D | STTTTST |
| Eb Lydian augmented (Lydian 5# or Lydian Sharp 5): | Eb F G A B C D Eb | TTTTSTS |
| F Lydian 7b (Mixolydian 4# or Mixolydian Sharp 4): | F G A B C D Eb F | TTTSTST |
| G Mixolydian 6b (Mixolydian Flat 6): | G A B C D Eb F G | TTSTSTT |
| A Aeolian 5b (Minor 5b or Minor Flat 5): | A B C D Eb F G A | TSTSTTT |
| B Superlocrian (Locrian 4b, Locrian Flat 4 or Diminished Whole Tone): | B C D Eb F G A B | STSTTTT |
| C Hypoionian (Melodic Minor): | C D Eb F G A B C | TSTTTTS |
| Jazz Scales with a common tonic, C |
| Dorian 2b (Dorian Flat 2): | C Db Eb G A Bb C | 1 b2 b3 4 5 6 b7 |
| Lydian augmented (Lydian 5# or Lydian Sharp 5): | C D E F# G# A B C | 1 2 3 #4 #5 6 7 |
| Lydian 7b (Mixolydian 4# or Mixolydian Sharp 4): | C D E F# G A Bb C | 1 2 3 #4 5 6 b7 |
| Mixolydian 6b (Mixolydian Flat 6): | C D E F G Ab Bb C | 1 2 3 4 5 b6 b7 |
| Aeolian 5b (Minor 5b or Minor Flat 5): | C D Eb F Gb Ab Bb C | 1 2 b3 4 b5 b6 b7 |
| Superlocrian (Locrian 4b, Locrian Flat 4 or Diminished Whole Tone): | C Db Eb Fb Gb Ab Bb C | 1 b2 b3 b4 b5 b6 b7 |
| Hypoionian (Melodic Minor): | C D Eb F G A B C | 1 2 b3 4 5 6 7 |
We thank Ari Dibyantara for correcting an earlier error in the table above.
You will see that we have offered a few more 'alternative' names for the scales that you may meet in other music theory texts.
We show below the G minor jazz melodic minor scale.
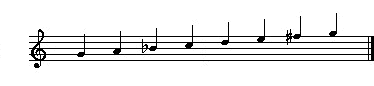
Various chords may be used to support this scale.

The important thing to remember is that, in jazz, chords and scales are considered equivalent. The wide use of harmonic extensions offers many more close relations between scales and chords than in a harmony based only on the standard triads with the addition of the occasional seventh.
Jazz is a broad term with many sub-categories and fusion styles. Maybe it would be more accurate to apply the name to the type of audience it attracts rather than the type of music being played. Jazz harmony often chooses as its foundation a 12-bar blues. Here is an example of simple 12-bar blues: This can be harmonised using the main major modes, the scales you get when you play the same note row (for example, the scale of C major), and start in on a different note (when played from D to D, you get the Dorian Mode). The major modes in a harmonised C major scale are shown below. | Chord | Start/End Note | Mode | Tonality | Played over | | 1 | C to C | Ionian | Major | Major or M7 chord | | 2 | D to D | Dorian | Minor | Minor or m7 | | 3 | E to E | Phrigian | Minor | Minor | | 4 | F to F | Lydian | Major | Maj7 | | 5 | G to G | Mixolydian | Major | Dominant 7, 13 or 9 | | 6 | A to A | Aeolian | Minor | Minor | | 7 | B to B | Locrian | Minor7b5 | m7b5 or diminished |
From the choice of chord one picks a particular scale, and vice versa; this mutual association gives jazz harmony chords and scales not found in other styles of music. We offer a jazz 12-bar to give an idea of what is possible. 4
4 | Bb13 | Eb9 | Bb13 | Fm9 Bbalt | Eb9 | Edim | Dm7 | G7b9 | Cm7 | F7#9 | Bb9 G7 | Cm7 F7#9 |
As we have seen above modes can also be derived from melodic minor scales. One particularly interesting example is the seventh mode of the melodic minor scale, one that starts and ends on the seventh note of the scale (for example, with C melodic minor, we play from B to B, the superlocrian mode). Its distinctive sound is heard in many jazz pieces and is main use is over an altered dominant seventh chord. For example, in the sequence above, it would be used on the last, F7#9, chord, and also the earlier G7b9 and F7#9 chords. In each case respectively, we use G superlocrian and F superlocrian. Applying the scales to the appropriate chords, and we produce the required harmony. 4
4 | Bb Mixolydian | Eb Mixolydian | Bb Mixolydian | F Dorian
Bb Superlocrian | Eb Mixolydian | E Diminished | D Dorian | G Superlocrian | C Dorian | F Superlocrian | Bb Mixolydian
G Mixolydian | C Dorian
F Superlocrian |
We thank Peter Francis for his help with this topic.
Before we leave this section on chords it would be useful to summarise the Lydian scales which are so important in jazz.
| Lydian scales |
| Lydian scale (or mode) | major scale with a raised fourth |
| scale that borrows the major key signature from a perfect fourth below or a perfect fifth above |
| Lydian augmented scale | major scale with raised fourth and fifth degrees |
| Lydian scale with a raised fifth degree |
| scale that borrows the ascending form of the melodic minor scale from a minor third below or a major sixth above |
Mixture scale
also called
Lydian b7, Mixolydian #4, Lydian-Mixolydian, Mixolydian-Lydian, Lydian Dominant | major scale with raised fourth and lowered seventh degrees |
| Lydian scale with a lowered seventh degree |
| Mixolydian scale with a raised fourth degree |
| scale that borrows the ascending form of the melodic minor scale from a perfect fourth below or a perfect fifth above |
| Synthetic Mixture #5 scale | major scale with raised fourth and fifth degrees along with a lowered seventh |
| Lydian scale with raised fifth and lowered seventh degrees |
| Lydian augmented scale with a lowered seventh degree |
| Mixture scale with a raised fifth degree |
|
|
|
Blues
::
|
Key word:
blues scales |
| 1 |
Blues
Music of certain genres have developed around certain chordal patterns and related scales. The blues scale supposedly has its roots in African American music dating back to the days of slavery, but the exact origins of its modern incarnation are unknown. Blues music uses the 'blues scale' one of which we show below. 
The blues scale is neither a minor nor a major scale but the internal dissonances provide the 'colour' that one associates with blues music - the 'blue' notes are the minor third and the 'flat five'.
You should note the unusual naming of the fourth note of this scale - really a diminished 5th - called the 'flat five'.
In vocal music, the second degree of the scale is often sung somewhere between an Eb and an E. In instrumental music, various techniques are employed to achieve the same effect, such as stretching the string while playing an Eb on a stringed instrument, lipping down an E on a wind instrument, or striking both the Eb and E simultaneously on a keyboard instrument. The flatted seventh and fifth also are not always sung or played exactly on the notated pitch.
Variations on the blues scale that include the natural third, fifth, or seventh can be used as well. Also, note that if the flatted fifth is omitted, the resultant scale is the minor pentatonic scale which we consider below. The minor pentatonic scale can thus be used as a substitute for the blues scale, and vice versa.
The beauty of the blues scale is that it can be played over an entire blues progression with no real avoid notes.
If you try playing lines based on this usage (for example, a C blues scale over a C7 chord) you get instant positive feedback, since almost everything you can do sounds good.
This unfortunately leads many players to overuse the scale, and to run out of interesting ideas quickly. One way to introduce added interest when using the blues scale is to use any special effects at your disposal to vary your sound. This can include honking and screaming for saxophonists, growling for brass players, or using clusters on the piano. Many draw attention to characteristic rhythms associated with 'blues' music. In fact, the best-known rhythm, called the 'eight-note triplet shuffle', is found also in jazz and swing. This rhythm is illustrated below. 
|
|
|
Bebop Scales
::
|
Key word:
bebop scales |
| 1 |
Bebop Scales
Bebop scales are not true scales in their own right, but scales that have had a chromatic passing note added to create an eight-note scale. This can be useful when improvising, in quavers (eighth notes), a scale passage can resolve to a chord note, or so that chord tones fall on a strong beat.
The major bebop scale is a major scale with an added raised fifth or lowered sixth. The C major bebop scale is shown below:  This scale can be used over major seventh or major seventh augmented chords.
The C major bebop scale can also be used as a bridge between chords in a progression such as:
Cmaj7-»Bm7(flat 5)-»E7-»Am
that is, the same scale can be played over the entire progression.
Another way of looking at this is to say that we are:
a. playing the C major bebop scale itself over the Cmaj7 chord
b. playing its eighth mode over the Bm7(flat 5) chord
c. playing its third mode over the E7 chord
d. playing its seventh mode over the Am chord.
These modes closely resemble the major, locrian, altered and minor scales respectively.
Note that we are using the C major bebop scale over a ii-»V-»i progression in A minor. In general, we can use the major bebop scale in any given key over a ii-»V-»i progression in the relative minor to that key. Other bebop scales include the dominant bebop scale, which is similar to the mixolydian mode but with an additional major seventh. The C dominant bebop scale is shown below: 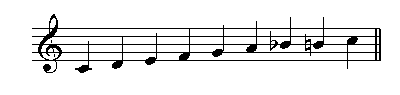 This scale can be used over dominant seventh chords. The major seventh is not really an avoid note if you use it as a passing tone between the C and Bb. It also serves as the raised fourth in the Fmaj7 chord that is likely to follow the C7 chord.
The bebop half-diminished scale is also based on a mode, the locrian mode, but has an added raised fifth.
There is also the minor bebop scale, which is a dorian scale with an added raised third. The C minor bebop scale is shown below:  This scale can be used over minor seventh chords, and is often used in minor key blues progressions to give more of a dominant seventh feel to the chords.
|
|
|
Pentatonic Scales
::
|
Key word:
pentatonic scales |
| 1 |
Pentatonic Scales
Found in many ancient cultures and traditions, including those of China, Indonesia, the native American Blackfoot people and both Scottish and English folk music traditions, the pentatonic scale is used widely also in jazz, blues, rock and classical music. It may be referred to as an anhemitonic pentatonic scale (anhemi meaning the absence of semitones or half steps), as for example both the major and minor forms of the pentatonic scale, or as a hemitonic scale, in which case one or more of the interval between successive notes will be semitone (half step).
In the pentatonic major scale only the 1st, 2nd, 3rd, 5th, 6th and 8th degrees of the major scale are used.
In the pentatonic minor scale only the 1st, 3rd, 4th, 5th, 7th and 8th degrees of the natural minor scale are used.
Pentatonic scales are transilient scales, scales that have fewer notes than heptatonic scales (for example, major scales, minor scales, Greek modes, etc.) and where, when ascending or descending, the melodic lines 'jump' over absent notes.
Note: the degrees of a pentatonic are named according to its related major or minor scale. So the fourth note of a pentatonic major scale is the 5th degree.
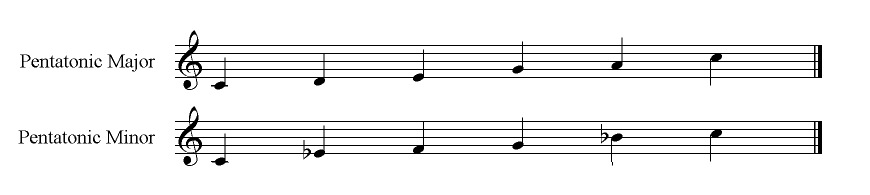
The perceptive reader may have noticed that we can arrange the notes of the pentatonic C major scale into an ascending sequence starting on A and thereby generate the pentatonic minor scale on A. This makes even clearer the relationship between these two scales, namely that they are each one of a pair of 'relative' scales, in exactly the same way that the C major scale is the relative major of the A natural minor scale.
In the our 1000+ Scales we give examples of many other pentatonic scales.
The Wikipedia page on Pentatonic scales explains the role of pentatonic scales in modern jazz and popular music generally.
Pentatonic scales are useful in modern jazz and pop/rock contexts because they work exceedingly well over so many chords diatonic to the same key, often better than the parent scale. So, for example, in the key of C major and over a C major triad (C-E-G) the note F, which is usually considered dissonant, becomes what in jazz is called an avoid note for that scale. Actually F can be allowed in some 'modal' musical contexts, where it is a characteristic note of the C Ionian mode. But using the major pentatonic scale offers an easy way out of any problem. The scale notes 1, 2, 3, 5, 6 (from the major pentatonic) are either major triad notes (1, 3, 5) or common consonant extensions (2, 6) of major triads. For the corresponding relative minor pentatonic scale, the scale notes 1, b3, 4, 5, b7 work in the same way, either as minor triad notes (1, b3, 5) or as common extensions (4, b7), all avoid being a semitone (half step) above a chord note.
|
|
|
|
The 'Minor Key' Problem
::
|
Key word:
minor key problem |
| 1 |
The 'Minor Key' Problem
You may already have been wondering why, if Western music can live with one major scale, it has felt it necessary to define three minor scales, the natural, harmonic and melodic. We have aready seen the melodic deficiency in the natural minor scale, namely the absence of a true 'leading note'. The harmonic and melodic scales address this problem by 'sharpening' or 'raising' the seventh in addition to making other changes to the natural minor scale. This was discussed in lesson 10. From a harmonic point of view, the 'sharpened' seventh turns the dominant chord from minor (Vmi) to major (Vma) increasing the feeling of 'suspension' from the dominant and increasing the 'pressure' on the dominant to 'resolve' to the tonic minor. Notice that the 'pressure' arises from the dominant and not from the tonic. The tonic can be major or minor but the 'feeling' remains. Occasionally 'fashion' led composers to favour the tonic major chord over the minor tonic at the end of a piece in a minor key. The tonic major chord was then called the Tierce de Picardie.  | | | Sharpened Seventh and the V-Imi Progression |
|
Sharpening the seventh of the minor scale on the dominant seventh also modifies the character of the dominant 7th - tonic cadence (V7-Imi). The sharpening heightens the 'need to resolve' although the cadence is not as 'strong' as when resolving to the tonic major. This is because the interval of a tone between F, the dominant 7th, and E flat in the tonic minor chord has a weaker feeling of 'suspension' than the interval of a semitone between F and E natural in the tonic major chord.  | | | Sharpened Seventh and the V7-Imi Progression |
|
The sharpened seventh affects other chords too. Let us harmonise the natural minor scale, with a sharpened 7th, first with diatonic triads and then with sevenths.  | | | Natural Minor, Sharpened 7th, Triads |
|
 | | | Natural Minor, Sharpened 7th, Sevenths |
|
The chord to look at carefully is that on the seventh degree of the scale. If the scale had been the harmonic minor, the A flat would have been 'raised' to an A natural. We have three possible chords on the seventh of the minor scale to consider: that on the natural seventh of the natural minor, that on the sharpened seventh of the harmonic minor (now no longer part of the natural minor scale) and the true diminished 7th on B natural. We illustrate and number all three below.  | | | Seventh Chords on the Seventh Degree of The Minor Scale |
|
This example shows the care one must take when numbering chords. In particular, if the seventh had been a natural then in the 'half diminished' chord it would have become a flat and in the 'diminished' chord it would have become a double flat, so that the chord 'looks' right on the page. One should, by now, begin to understand why notation not only tells us about the 'melodic' form of the music but clarifies the 'harmonic' structure too, at least if the standard notational 'conventions' are followed. Sharpening the seventh has one last interesting effect on the tonic minor chord. The minor 3rd combined with the major 7th is the origin of its name, the minor/major seventh. It may be used in chordal progressions in both major and minor keys. We leave further discussion of minor chords until lesson 31 entitled Key Centres.
|
|
|
Altered Chords
::
|
Key word:
altered chords |
| 1 |
Altered Chords
Any chord, whether major, minor, augmented or seventh, can be 'modified' or 'altered' thereby changing its character or 'colour'. In particular, with the dominant seventh which is wholly characterised by three notes, the root, major third and minor seventh, the fifth, ninth, eleventh and thirteenth may be altered. Raising or lowering by a semitone the notes of the chord and its extensions may change its dissonance. This increases the 'tension' of the chord and increases the sense of release as one moves to a less dissonant chord, for example the tonic. Care must be taken that these altered chords are correctly numbered and later we look at a few examples to show how this is done.
In any chord, a note is said to be altered if it differs from that found in a major scale based on the key note of the chord. By making reference to the major scale, a process known as parallel major comparison, notes not in the scale may be seen as inflected, that is they have been 'sharped' (raised) or 'flatted' (lower). By convention, certain notes are never thought of in this way. The most obvious example is the root itself. If it is 'sharped' or 'flatted' we usually use the new note to establish the new standard major scale to which all the remaining notes are then compared.
The convention is extended also to the 3rd (important in determining whether a chord is major or minor) and 7th (because of its role in dominant chord formulae) degrees of the scale. The 6th degree is excluded unless it appears one octave higher as a 13th. However, both the 2nd (and its octave equivalent, the 9th) and the 4th (and its octave equivalent, the 11th) may be 'altered' as can the 5th. Whether, in fact, particular alterations make harmonic sense often depends on various enharmonic relationships: for example a 'sharped' 2nd degree is enharmonically equivalent to a 'flatted' 3rd which is we have already discovered is excluded.
The standard way of writing altered seventh chords is to identify the quality of the chord (i.e.whether major, minor or dominant) and then add the modified note in brackets. If more than one note is altered both are shown, one above the other in one pair of brackets, with the widest interval at the top. If the fifth has been raised then the usual symbol (+ for augmented) appears before the 7. So: A9(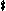 11) represents a ninth chord on A with the root, a major 3rd, a perfect 5th, a flattened 7th, a major ninth and a sharpened 11th; 11) represents a ninth chord on A with the root, a major 3rd, a perfect 5th, a flattened 7th, a major ninth and a sharpened 11th;
while A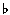 9( 9(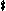 11) represents a ninth chord on A 11) represents a ninth chord on A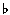 with the root, a major 3rd, a perfect 5th, a flattened 7th, a major ninth and a sharpened 11th. with the root, a major 3rd, a perfect 5th, a flattened 7th, a major ninth and a sharpened 11th.
|
G7( | 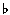 9 9 | 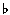 5 5 |
| ) | represents a seventh chord on G, with the root, major 3rd, diminished 5th, minor 7th and minor 9th. The main purpose of alternating chords is to increase the effectiveness in a progression. We have seen already how a dominant seventh is more effective than a dominant in a perfect cadence. The examples below show how altered fifths, ninths, elevenths and thirteens can work - listened to the top note of each chord in each example. 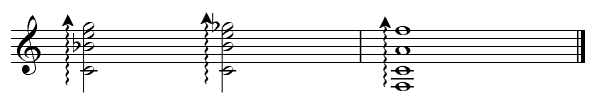 | | | Lowered Fifth of the Dominant |
|
 | | | Raised Fifth of the Dominant |
|
 | | | Lowered Ninth of the Dominant |
|
 | | | Raised Ninth of the Dominant |
|
 | | | Raised Eleventh of the Dominant |
|
 | | | Lowered Thirteenth of the Dominant |
|
|
|
|
Neapolitan Sixth
::
|
Key word:
neapolitan sixth |
| 1 |
Neapolitan Sixth
One 'named' altered chord is the Neapolitan Sixth or Phrygian II which is the first inversion of a major chord on the flattened (sometimes described as 'lowered') supertonic, the second degree of the major and minor scales used. This is a member of the family of Neapolitan chords. It is also called Phrygian II It is called 'sixth' because it is most commonly used in first inversion (or 6/3 position) and is named symbolically as N6. It is commonly used to reach the dominant chord or the tonic chord in second inversion when performing a cadence. In the key of C the flattened (or 'lowered') supertonic is D flat, the major chord would be D flat, F and A flat. The first inversion has F in the bass. In either form, it is the most common way of modulating down a semitone. It is very occasionally used in root position, N, or in second inversion, N64, (in either case it is then called a Neapolitan chord). When using a Neapolitan sixth in major keys, its fifth should be lowered in order to create the same chord accidentals as in the minor key. The examples illustrated below are in D minor and F major. 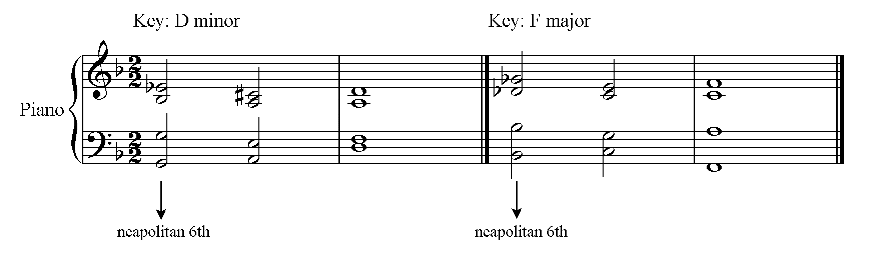 One striking use of the Neapolitan Sixth chord occurs in the Andante of Schubert's Symphony in C major. Schumann praised this particular passage in his review published in Neue Zeitschrift für Musik (1840). The alternating dominant chords on C, F and D resolve via a Neapolitan Sixth to the principal theme heard on the oboe in bar 160.
Reference: Neapolitan Sixth
|
|
|
Symmetrical Scales
::
|
Key word:
symmetrical scales |
| 1 |
Symmetrical Scales
It is a small matter to construct scales that contain the notes of altered chords. Set out horizontally the notes of any particular chord and complete the scale by filling in any gaps. Dominant chords are the most common base for such scales. We will leave further discussion of these 'altered scales' until our lesson on key centres. There are, however, a number of scales that we can look at now, namely those built up from a repeating pattern of intervals. We have already seen one such scale, the chromatic scale in lesson 11. With a repeating whole tone, we build the Whole Tone Scale. 
The intervals are constant so that any of the six notes could be nominated the tonic. The scale includes notes that could function as root, major third, and the seventh of a dominant 7th plus a ninth. The scale can therefore be thought of as the 'altered' scale of a dominant ninth chord with an augmented fifth (i.e. a V+9 chord).
This idea of 'associating' one scale with other by identifying notes 'in common' (or 'in parallel') can be extended, as the table below shows.
The whole tone scale, for example, can be viewed from many different 'parallel' standpoints.
| whole tone scale | 'parallel' scale | notes, or their alterations, that the two scales have in common |
| C Whole Tone scale | C Major scale | first, second, third, raised fourth, raised fifth and lowered seventh degrees |
| C Whole Tone scale | Lydian scale | first, second, third, fourth, raised fifth and lowered seventh degrees |
| C Whole Tone scale | Lydian augmented scale | first, second, third, fourth, fifth and lowered seventh degrees |
| C Whole Tone scale | Mixture scale | first, second, third, fourth, raised fifth and seventh degrees |
| C Whole Tone scale | Synthetic Mixture #5 scale | first, second, third, fourth, fifth and seventh degrees |
Another pattern alternates tone and semitone intervals producing the Diminished Scale. If the pattern is tone-semitone one gets the chord scale of a diminished seventh chord also known as the Octatonic Scale, much used by Stravinsky. Richard Warford points out that it is also one of Messiaen's "modes of limited
transposition" as it can only be transposed up or down a semitone (or half-step) twice. After a third transposition one recovers the original scale but with a new root. In fact, as Nuno André Novo has pointed out, in equal-temperament, there are only three forms of the diminished scale. Those built on roots C, Eb, F# and A are identical, those built on roots D, F, Ab, B are identical, as are those built on roots Db, E, G and Bb 
If the pattern is semitone-tone one gets a Dominant Diminished Scale, the chord scale for functioning dominant chords with altered ninths and natural fifths.

We will return to these matters in Lesson 31.
We complete this section by summarising the categorisation of symmetrical scales according to the way they are constructed.
| alternating-interval symmetrical scales |
| augmented scale form one | alternating-interval symmetry of minor third / semitone (half-step) |
augmented scale form two
inverted augmented scale | alternating-interval symmetry of semitone (half-step) / minor third |
eight-note diminished scale
octatonic scale | alternating-interval symmetry of tone (whole-step) / semitone (half-step) |
eight-note dominant scale
dominant diminished scale | alternating-interval symmetry of semitone (half-step) / tone (whole-step) |
| constant-interval symmetrical scales |
whole tone scale
six tone scale | constant-interval symmetry of the tone (whole step) |
| chromatic scale | constant-interval symmetry of the semitone (half-step) |
|
|
|
Table of Useful Scales
::
|
Key word:
table of useful scales |
| 1 |
Table of Useful Scales
We have prepared a list of 1000+ scales which will now be found on our 1000+ Scales Page.
|
|
|
Non-Harmonic Notes
::
|
Key word:
non-harmonic notes |
| 1 |
Non-Harmonic Notes
Not all notes in a piece of harmony have anything to do with a particular chord or chord progression. These are called non-harmonic notes, non-chordal notes, non-chord notes or non-essential notes. | Non-Harmonic, Non-Chord, Non-Chordal or Non-Essential Notes |
| classification | symbol | type | description |
passing notes
passing tones (US)
transient notes
nota di passaggio (Italian s.)
Durchgangsnote (German s.)
Durchgangston (German s.)
Übergangsnote (German s.)
note de passage (French s.) | p | melodic | notes that pass by a tone (step) or semitone (half-step) between chord notes. |
neighbouring notes
neighboring tones (US) | n | melodic | notes that leave and return to the same chord note by a tone (step) or semitone (half-step). |
appoggiatura
notes de gout (French) | a | melodic | a note that is approached by leap, but resolves to a chord note by a tone (step) or semitone (half-step) - the resolution often in the opposite direction to the leap. |
| escape note | e | melodic | the opposite of an appoggiatura, being approached by a tone (step) or semitone (half-step) and resolving to a chord note by a leap. |
suspension
prolongation | s | harmonic | a note that is held over, that is approached by itself, and resolved to the chord note by stepping down a tone (step) or semitone (half-step) after the chord is played. |
| retardation | r | harmonic | a note that is held over, that is approached by itself, and resolved to the chord note by stepping up a tone (step) or semitone (half-step) after the chord is played. |
anticipation
syncopation | ant | harmonic | the chord note arrives before the chord is played. It is usually approached by tone (step) or semitone (half-step). |
pedal note
pedal point | ped | harmonic | a repeating note or note held over while the harmony changes. |
auxiliary note
nota ausiliare (Italian)
Nebennote (German)
note secondaire (French) | aux | | a note that relates to a chord note but may not be a neighbouring note. |
changing notes
neighbor group (US)
changing tones (US)
nota cambiata (Italian s.)
Wechselnote (German s.)
Wechselton (German s.)
note changée (French s.) | c.n., n. gr. or c.t. | melodic | two notes, one that leaves the chord note by a tone (step) or semitone (half-step), then leaps to the next non-harmonic note by skipping over the chord note, before resolving to the same chord note by a tone (step) or semitone (half-step). |
References:
Non-chord tones with illustrated examples
Non-harmonic notes with illustrated examples
Note: the term 'appoggiatura' defined above is a description for a non-harmonic note, and should not be confused with an 'appoggiatura' used as an ornament which is discussed in lesson 23. The French term notes de gout or the English term 'diminutive notes' may be applied to the non-harmonic appoggiatura as well as to other ornamental notes. The term 'syncopation' as a description for a non-harmonic note, should not be confused with the term 'syncopation' used when discussing rhythm.
|
|
 :: next lesson :: next lesson
| |
 :: next lesson
:: next lesson


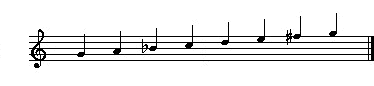




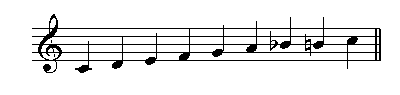

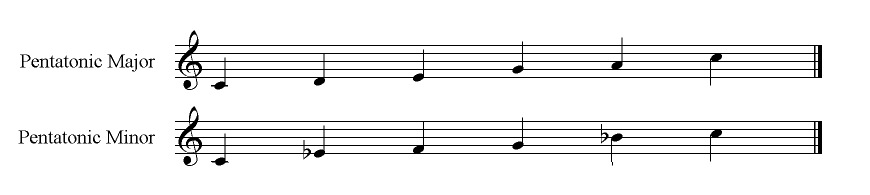





 11) represents a ninth chord on A with the root, a major 3rd, a perfect 5th, a flattened 7th, a major ninth and a sharpened 11th;
11) represents a ninth chord on A with the root, a major 3rd, a perfect 5th, a flattened 7th, a major ninth and a sharpened 11th; 9(
9(